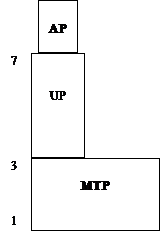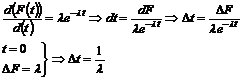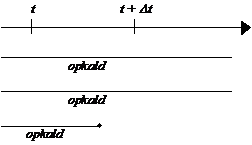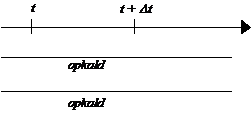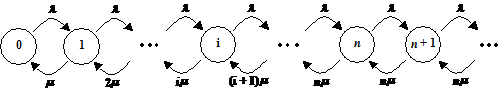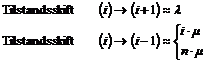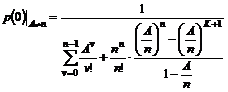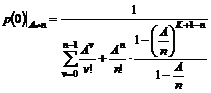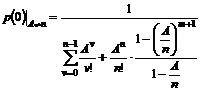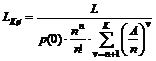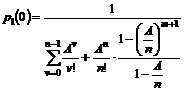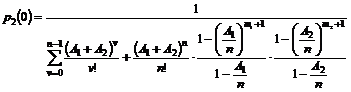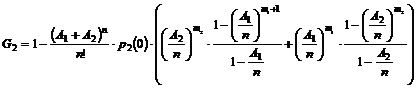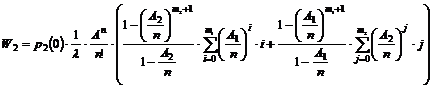1. Problemstilling........................................................................................................
2. Løsningsmetode..........................................................................................................
3. GLAD-systemet.............................................................................................................
3.1 GLAD systemets
opbygning............................................................................................................................................
3.2
Protokolreferencemodeller............................................................................................................................................
3.3 Kort beskrivelse af
GLAD............................................................................................................................................
3.4 AXE....................................................................................................................................................................................
3.5 IN.........................................................................................................................................................................................
3.6 OPS.....................................................................................................................................................................................
3.7 AIP......................................................................................................................................................................................
3.8 OP118 tjenesten...............................................................................................................................................................
3.8.1 Kø typer.....................................................................................................................................................................
3.9 OP118
Tilstandsdiagram..............................................................................................................................................
4. Statistik.........................................................................................................................
4.1 Løsningsmetode for
statistik........................................................................................................................................
4.2 Hvorfor anvendes
statistik...........................................................................................................................................
4.3 Forslag til
statistikmålinger.........................................................................................................................................
4.4 Realisering af
statistikmålinger..................................................................................................................................
4.4.1 Generelt om
målinger............................................................................................................................................
4.4.2 De enkelte
målinger................................................................................................................................................
4.5 TDK’s statistik.................................................................................................................................................................
4.6 Sammenligning af
vores forslag og TDK’s statistik..............................................................................................
4.6.1 Sammenligninger
af målingerne........................................................................................................................
4.6.2 Endeligt forslag
til målinger................................................................................................................................
4.6.3 Forslag til
tabel........................................................................................................................................................
4.6.4 Delkonklusion...........................................................................................................................................................
5. Introduktion til
teletrafikteori.............................................................
5.1 Løsningsmetode...............................................................................................................................................................
5.2 Generelt om
teletrafikteori..........................................................................................................................................
5.2.1 Generelt om
ventetidssystemer............................................................................................................................
5.2.2 Statistik og
sandsynlighedsregning.....................................................................................................................
5.2.3 Anvendte begreber
inden for teletrafikteori....................................................................................................
5.2.4 Karakteristiske
størrelser og enheden ”erlang”.............................................................................................
5.2.5
Eksponentialfordelingen, intensiteten l............................................................................................................
5.2.6
Ligevægtssandsynligheder....................................................................................................................................
5.2.7
Springintensitetsdiagrammer..............................................................................................................................
5.2.8
Ventetidssystemer....................................................................................................................................................
6. Udvidelse af M/M/n
modellen..........................................................................
6.1 M/M/n/K Model,
OP118 uden overløb......................................................................................................................
6.1.1 Delkonklusion...........................................................................................................................................................
6.2 M/M/n/(m1,m2)
Model, OP118 med overløb.............................................................................................................
6.2.1 Delkonklusion...........................................................................................................................................................
6.3
Sammenligning af M/M/n/K og M/M/n/(m1,m2).......................................................................................................
6.4 Numeriske
simuleringer af M/M/n/K Modellen.....................................................................................................
6.4.1
Tilstandssandsynligheder ved beregning..........................................................................................................
6.4.2
Simuleringsprogram..............................................................................................................................................
7. Konklusion...................................................................................................................
Bilag 1,
Fremkommeligheds krav.....................................................................
Bilag 2, Forkortelser...............................................................................................
Bilag 3, Tidsplan............................................................................................................
Bilag 4, Litteratur
henvisninger og Interviewede personer....
Bilag 5,
Programudskrift......................................................................................
Bilag 6, Diskette..........................................................................................................
Forord.
Inden for teleteknik findes der mange indforståede
forkortelser. Derfor har vi i Bilag 2 vedlagt en liste over anvendte
forkortelser. Desuden er der mange engelske udtryk som ikke kan oversættes
direkte til dansk uden at de lyder forkert. Der er derfor, i enkelte tilfælde,
anvendt engelske udtryk i rapporten.
Litteraturhenvisninger refereres med firkant
parenteser [], interviewede personer er refereret med krølle parenteser {} og
som formelhenvisninger anvendes almindelige parenteser () (undtagelser heraf er
henvisninger imellem de enkelte tilstande i forklaringen til tilstandsdiagrammet
i kapitel 3.9,
eller når der, som her, indskydes en bemærkning i parentes). Når udtryk fra
litteraturen er vist, så vises det med [L]-nn eller [L]-sMM hvor [L] er
litteraturhenvisningen, nn er formel nummer og MM er sidenummer.
Synopsis.
Denne rapport gennemgår en analyse af TDK’s
servicetelefoncentral, hvorved det er muligt at opstille et tilstandsdiagram
over en udvalgt tjeneste. Dette tilstandsdiagram anvendes herefter til at
vurdere hvilke størrelser, der kan være interessante at bruge i en
statistikopsamling. Dette munder ud i et forslag til en forbedret
statistikopsamling i forhold til TDK’s.
Herefter introduceres teletrafikteorien og
det vises, hvordan springintensitetsdiagrammer udvikles, samt hvordan
matematiske modeller opstilles. Dette gøres på grundlag af et
springintensitetsdiagram. Derudover vises det, hvordan numeriske beregninger foretages
på disse matematiske modeller vha. rekursive metoder, for at undgå at skulle
regne med meget store tal. Disse metoder er desuden implementeret i et program.
Resultatet af den matematiske analyse er et
godt grundlag for en evt. viderebearbejdning.
Der skal i dette projekt fortages en
kvantitativ analyse af trafikafvikling i en servicetelefon-central. Det primære
mål er at nå frem til en metode/metoder til dimensionering og/eller optimering
af de eksterne ressourcer, såsom talemaskiner og telefonister. Det indbefatter,
at der så vidt muligt laves en matematisk model af køsystemet i OP118.
Yderligere ønskes en analyse og evt. forslag til forbedring af principper for
nuværende statistikopsamling.
For at få indblik i
teletrafik vil forskellige tjenester, trafikmønstre, trafikmængder, opbygning
af platformen for servicetelefonen, samt kaldsfordelingsprincippet blive
grundigt undersøgt. Derudover vil undervisningsmateriale om teletrafikteori [1]
blive studeret.
Projektets omfang
begrænses ved at de eksterne ressourcer koncentreres til OP118 tjenesten. For
at få et overblik, vil GLAD (Gain Landsdækkende Danmark) systemet blive
beskrevet, og der vil blive lavet et tilstandsdiagram, for et kalds mulige
skæbner i OP118 servicen.
Det vurderes, at
det efter endt studie af GLAD systemet, vil være muligt at lave en
løsningsmetode for statistikopsamling og optimering.
Herefter bliver de
vigtigste elementer i teletrafikteorien kort gennemgået og teorien anvendes til
at beskrive køsystemet i OP118 vha. matematiske modeller.
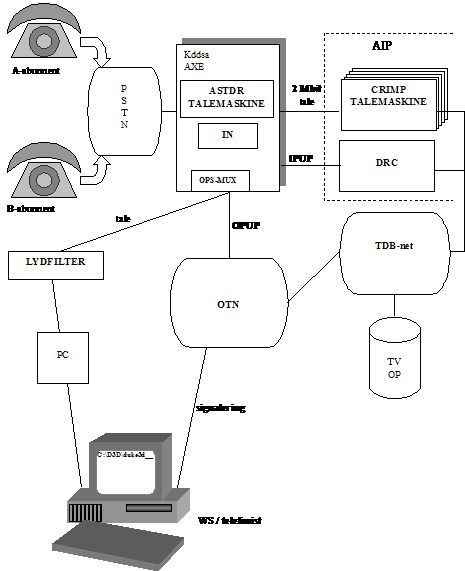
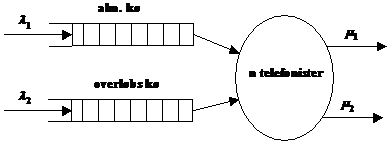
I de følgende
afsnit bliver GLAD systemet beskrevet. Først kort om det overordnede system (se
Figur 3-1 ), derefter introduceres de
kommunikations protokolreferencemodeller, der anvendes i GLAD systemet. Senere
udspecificeres de vigtigste dele i systemet. Beskrivelsen sker på grundlag af
[2], [3], [5], {1} og {2}.
Dette gøres for at
give et overblik over hvordan systemet fungerer, for derefter at kunne udvikle
et tilstandsdiagram. Tilstandsdiagrammet har til formål at være udgangspunkt i
en analyse af statistikopsamlingen (se kap 4).
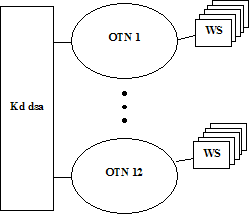
Der findes i
Danmark to specialcentraler, der bruges til at behandle servicekald, såsom
oplysning (OP118) vej- og vejrmeldinger, klokken osv. Disse to centraler er
benævnt kddsa, Kolding digitale special central, og khdsa, København digitale
special central og forefindes henholdsvis i Kolding og København, hvor Kddsa
tager sig af abonnenter vest for Storebælt, og khdsa øst for Storebælt. Abonnenterne
kommer i forbindelse med en af disse centraler via det offentlige telefonnet,
PSTN (Public Switched Telephone Network). PSTN skal her opfattes som hele
telefonnettet, med lokalcentraler og de fysiske forbindelser. Det er f.eks. via
PSTN, at to abonnenter kommer i forbindelse med hinanden.
Når en kunde har
kaldt OP118 (OPlysningen nr. 118) bliver kaldet dirigeret gennem PSTN til den
ene af de specielle AXE centraler, afhængig af kundens geografiske placering.
AXE centralen er opdelt i flere delsystemer, som vist på Figur 3-1, bl.a. IN (Intelligent Network) og OPS (OPerator
Subsystem), der sørger for, at kunden får forbindelse til en telefonist, der
sidder ved en WS (Work Station) tilsluttet OTN (Operator Terminal Network).
Denne telefonist kan efterkomme kundens ønsker om information ved at hente data
fra en database tilsluttet netværket.
Efter endt
betjening kan telefonisten selv oplyse om f.eks. et B-nummer, eller der kan
skiftes til audio release, hvor IN via DRC (Distributed Ressource Controller)
får CRIMP talemaskinen til at oplæse B-nummeret. AST-DR talemaskinen anvendes
til velkomstmeddelelser. Af Figur 3-1 fremgår det desuden, hvilke kommunikations
protokoller, der bliver anvendt enhederne imellem. Derfor beskrives
protokolreferencemodeller kort i næste afsnit på baggrund af [5].
Der er i de seneste år, med de mange
forskellige computere og intelligente enheder, opstået et behov for at kunne
kommunikere enhederne imellem. Da disse enheder kan være af meget forskellig
art, både hvad angår software, platform og fysiske egenskaber, har det været
nødvendigt at lave en standardiseret kommunikationsbeskrivelse. Med de mange
enheder, der eksisterer, vil der være et væld af sammenkoblingsmuligheder, hver
med en detaljeret interface specifikation. For at undgå disse mange
specifikationer, er der udformet en standardiseret protokolreferencemodel
(PRM). Denne PRM forudsætter, at enheden kan opdeles i procesorienterede og kommunikationsorienterede
funktioner, som vist i Figur
3-2.
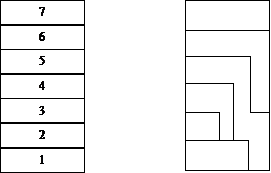
Kommunikationen mellem to enheder kan være
kompliceret, og derfor anvendes der flere forskellige protokoller til
implementering af kommunikationsfunktionerne. En PRM kan have flere forskellige
udformninger, og i Figur
3-3 vises to forskellige PRM.
Figuren til venstre viser OSI (open system
interconnection) og til højre ses DOD (department of defence) modellen. I OSI
er de enkelte delsystemer lagdelt, således at et lag kun kan kommunikere med de
to tilstødende lag, mens delsystemerne i DOD modellen kan kommunikere med
hirakisk lavere beliggende lag.
I GLAD systemet anvendes OSI modellen, med
visse modifikationer, som vises sidst i kapitlet. Pga. lagdelingen i OSI
modellen og dellagenes uafhængighed af andre end nabolagene, kan de enkelte lag
betragtes som moduler, der frit kan modificeres, når blot interfacingen til
nabolagene er som tidligere. Lagdelingen medfører tillige at to åbne systemer
med forskellige implementering af lagenes funktioner kan kommunikere, hvis blot
de enkelte lag har en fællesmængde i den udvekslede information, samt hvis der
kan opnås enighed om specifikationerne for data transmission i det fysiske
medium. To systemer, der kommunikerer indbyrdes kaldes peer-end systemer.
OSI modellen er inddelt i 7 lag som vist i Figur 3-4.
I det følgende beskrives de enkelte lags
funktioner, samt de funktioner de enkelte lag tilbyder nabolaget ovenover.
Dette gøres fra det fysiske medium (oftest kaldet lag 0) og op til
applikationslaget. Denne funktionalitet virker selvfølgelig også den anden vej,
f.eks. kan lag 1 også oversætte binære data til fysiske signaler, der er
tilpasset det fysiske medium.
|
Lag.
|
Beskrivelse af laget.
|
|
0 Det
fysiske medium
|
Transporterer information mellem
enhederne. Det kan f.eks. være gennem kabler, lysledere, æteren (radio) osv.
|
|
1 Det
fysiske lag
|
Oversætter informationen fra det fysiske
lag til binær data som tilbydes lag 2. Lag 1 er dermed et interface til det
fysiske medium.
|
|
2 Datalænke
laget
|
Strukturerer bitsekvenser i rammer eller
datapakker. Disse rammer forsynes med specielle start og stop bitsekvenser.
|
|
3 Netværks
laget
|
Tilbyder overførsel af data mellem to
vilkårlige enheder i det samlede netværk. Netværkets enkelte enheder
adresseres således at netværkslaget kan dirigere datapakkerne til den rigtige
enhed.
|
|
4 Transportlaget
|
Tilbyder pålidelig og ”cost-effective”
overførsel af meddelelser mellem transportlagene i de to peer-end systemer.
|
|
5 Sessionslaget
|
Tilbyder applikationsprocesser i de to
peer-end systemer en struktureret dialog, bestående af en udveksling af
meddelelser. Det kan bl.a. bestå i at bestemme, hvem der har retten til at
udføre forskellige funktioner, og i at genskabe dialogen efter midlertidige
afbrydelser.
|
|
6 Præsentationslaget
|
Tilbyder applikationsprocesserne en
veldefineret syntaks af de udvekslede data. Det kan dreje sig om at oversætte
eller konvertere peer-end systemets data format til formatet på de
transmitterede data.
|
|
7 Applikationslaget
|
Dette lag tilbyder en meningsfyldt
semantik af applikationslagets udvekslede data. Desuden tilbyder laget den
samlede service til kommunikation mellem applikationsprocesserne og dermed
også funktioner, der ikke varetages af de underliggende lag.
|
I OSI modellen beskrives lagene 1 til 3 ofte
som lavniveau lagene og lagene 4 til 7 som højniveau lagene. Denne inddeling er
særlig nyttig, når der kommunikeres mellem to systemer, der ikke er direkte
forbundet. Se Figur
3-5 herunder.
Som det fremgår af figuren, sker
kommunikationen mellem de to end-systemer via et mellemliggende relæpunkt, der
her videresender de sendte meddelelser. Da det kun er de tre nederste lag
(eksklusiv lag 0), der er nødvendig for at meddelelser kan dirigeres til den
rigtige modtager i et netværk, udfører relay-systemet kun funktionerne svarende
til disse tre lag. Lagene 1 til 3 kaldes derfor netværksfunktioner. De
resterende lag, 4 til 7, kaldes end-to-end funktioner da disse funktioner
udelukkende udføres i de to end-systemer.
I GLAD systemet anvendes en PRM der kaldes
system 7, og som er opbygget efter samme princip som OSI modellen. De tre
nederste lag, netværksfunktionerne, er samlet i
MTP (Multi Transfer Point), og har samme funktion som netværksfunktionerne
i OSI modellen. De resterende lag, 4 til 7, udgør UP (User Part), som har samme
funktionalitet som end-to-end delen i OSI modellen. Den software, der benytter
sig af de af modellen tilbudte funktioner, er placeret i AP, Application Part.
|
|
|
Figur 3-6, System 7 modellen.
|
På de næste tre figurer vises eksempler på,
hvordan kommunikationen foregår mellem forskellige delsystemer i GLAD ved at
implementere system 7 modellen. INAP (intelligent networks application part),
IPUP (intelligent peripheral user part) og OPUP (operator user part) er
kommunikationsprotokoller, der ikke beskrives nærmere i denne rapport.
Kommunikationen mellem SSF (IN) og PSTN sker
efter to forskellige modeller, afhængig af, om der er tale om en almindelig
forbindelse eller ISDN. Hvis der er tale om telefoni, anvendes TUP (telephone
user part), og i tilfælde af en ISDN forbindelse bruges ISUP, ISDN User Part.
|
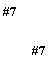 
|
|
Figur
3-7,
Kommunikationen mellem SSF og PSTN.
|
Kommunikationen mellem SCF og SSF (IN) sker
som vist i Figur
3-8. Som UP anvendes TCAP
(transaction capability application part), som ikke beskrives nærmere, og AP
bruger INAP protokollen.
|
|
|
Figur
3-8,
Kommunikationen mellem SCF og SSF.
|
SSF kommunikerer med DRC og OTN som
skitseret i Figur
3-9. SSF bruger IPUP protokollen,
når der kommunikeres med DRC, og OPUP protokollen, når der kommunikeres med
OTN.
|

|
|
Figur
3-9,
Kommunikationen mellem SSF og DRC/OTN.
|
Inden en nærmere beskrivelse af GLAD
systemet, introduceres systemet her i korte træk for at give et overblik.
Systemet vil blive beskrevet ud fra Figur
3-1 og de enkelte systemer vil derefter blive gennemgået mere uddybende
i de efterfølgende kapitler.
Hver digitalcentral har en hovedenhed AXE,
der behandler og fordeler de indkommende opkald. OPS er den enhed der
distribuerer de indkommende kunder til en ledig telefonist gennem OTN (operator
terminal network), og derudover behandler OPS også de forskellige køtyper. Når
OPS prøver at skabe en forbindelse til en telefonist i OTN, vil dette gøres med
en vis prioritering.
Den enkelte telefonist sidder i en
telefonistgruppe. Denne gruppe kan klare
flere forskellige servicetyper, hvor af OP118 er en af dem. Dette er gjort for
at gøre systemet så fleksibelt som muligt Dog er der, for at mindske
betjeningstiden, lavet en prioritering af de forskellige servicetyper, som den
enkelte telefonistgruppe kan modtage. For at sikre, at de forskellige services
bliver betjent, skal de minimum være af højeste prioritet i en af telefonistgrupperne.
Udover prioritering vil OPS også prøve at finde den telefonistgruppe, der har
den mindste a-værdi,
dvs. den telefonistgruppe der er mindst belastet, se kap 3.6 hvor denne
problemstilling er nærmere beskrevet.
Er en telefonist ikke ledig, vil der opstå
en kødannelse. Her vil OPS og IN sørge for at kunden får kømeldinger fra
talemaskinen i ASTDR i AXE. Den opståede kø vil blive afviklet efter FIFO
(first in first out) princippet. Kunden kan dog højst være i køen i 90 sek. ± 30
sek., hvorefter forbindelsen vil blive afbrudt pga. netovervågningens
linienedkobling, der indtræffer når B-abonnenten ikke svarer, eller har lagt
på, mens A-abonnenten stadig opretholder forbindelsen. Ved overløb (fyldt kø),
eller hvis køen afvises, f.eks. pga. at den længste ventetid i køen er over 40
sek., vil der være mulighed for viderestilling til den anden central. Dette vil
ske i IN (se kapitel 3.5).
Overløb kan kun ske for nye opkald, og ikke for opkald der i forvejen er
overløbskald.
OTN, der gennem GW (gate ways), , har
forbindelse med AXE, består af flere OTN-ringe, i alt 28, hvoraf de 12 er
tilsluttet kddsa og de 16 khdsa, (se kap. 3.6).
Disse OTN-ringe er forbundet indbyrdes i netværk, der er placeret henholdsvis
vest og øst for Storebælt, og de har hver tilkoblet op til 30 WS (work
stations), der hver betjenes af en telefonist. Udover GW-forbindelsen, der
bruges til dataoverførsel, er der også en taleforbindelse fra WS til AXE. Det
er igennem denne forbindelse, samtalen mellem kunden og telefonisten
transmitteres.
Efter endt betjening, af eksempelvis et
OP118 kald, er der mulighed for en viderestilling via OPS til en talemaskine i
AIP (advanced intelligent peripheral). Talemaskinen CRIMP har forbindelse til
OPS i AXE via DRC, der samtidig er den enhed, der er bestemmende for, hvad
CRIMP skal udføre. Talemaskinen bruges her til oplæsning af det fundne
telefonnummer ved audio release.
For at gøre betjeningen nemmere for telefonisterne,
findes der forskellige skærmbilleder, alt efter hvilket servicekald, det drejer
sig om. Hvis en kunde efter audio release ønsker at tale med en telefonist
igen, OFB (operator fall back), følger disse skærmbilleder kunden, således at
en ny telefonist får samme informationer som den første telefonist, da det ikke
nødvendigvis er den samme telefonist, der kommer i forbindelse med kunden igen.
AXE’en er en
digital telefoncentral fra Ericsson. Der findes flere forskellige versioner af
AXE centraler, f.eks. AXE TS18R2 og AXE TS30, hvor version TS18R2 anvendes på
lokalcentraler og version TS30 anvendes i AXE kddsa og AXE khdsa. AXE’en
udfører to vigtige funktioner, multiplexing/switching OPS (operator subsystem)
mellem de forskellige enheder, samt et script IN (intelligent network), der
håndterer kaldene. AXE’en er modulopbygget, hvilket betyder, at der kan
foretages servicearbejde på de enkelte moduler, uden det forårsager
forstyrrelser i den del af centralen, der ikke bruger dette modul.
IN’en består af
flere moduler, der arbejder sammen som i et netværk. Disse moduler kan modtage
informationer fra abonnenten og reagere på basis af disse informationer, deraf
navnet intelligent netværk. Det er f.eks. gennem IN, at man kan opsamle data om
trafikken i forskellige punkter, og det er IN der håndterer takseringen af
opkaldene. IN’ens overordnede funktion er at styre et kaldsforløb og at føre
kontrol mellem enhederne i GLAD systemet.
IN’ens funktioner
kan opdeles i to grupper
SSF, Service Switching
Function.
SCF, Service Control Function.
Disse to funktioner
er samlet i en SSCP, da kommunikationen foregår internt. Kommunikationen mellem
centralerne, dvs. ekstern kommunikation, sker i SCP Dette vil dog ikke blive
beskrevet nærmere i dette projekt.
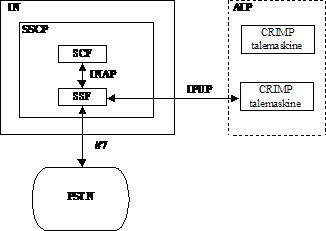
I Figur 3-10 er det vist hvordan IN er
tilsluttet PSTN og AIP, samt hvilke protokoller der jf. kap. 3.2 anvendes enhederne
imellem.
|
|
|
Figur 3-10 Skitse
over kommunikationsvej mellem IN, PSTN og AIP.
|
Når et kald
ankommer fra PSTN, sker kommunikationen mellem PSTN og SSF efter #7 protokollen
(se Figur 3-7). Herefter sendes kaldsdata fra SSF
til SCF efter INAP protokollen. SCF og SSF udveksler instruktioner alt efter
kaldstypen. F.eks. kan SCF sende instruktioner til SSF, der skal videre til
DRC, hvis der skal bruges ressourcer fra en CRIMP talemaskine. Desuden sørger
IN for, ved CC (call completion), at afbryde forbindelsen til telefonisten for
at undgå den særlig høje taksering der er ved servicekald, og opretter en ny
forbindelse til B-abonnenten.
OPS er som før
beskrevet den del af AXE, som forsøger at skabe en forbindelse til en ledig
telefonist, behandle de forskellige køtyper og omstille fra en telefonist til
AIP.
OPS er opdelt i tre
blokke bestående af COP (common operator platform), TOF (toll operator
functions), SOF (dervice operator functions).
- COP er den enhed, der tager sig af de
grundlæggende funktioner, såsom håndtering af kommunikationen mellem AXE og
OTN, og at holde styr på de forskellige terminaler i OTN. Derudover udvælger
COP den enkelte telefonist, udfra fastsatte kriterier og prioriteringer. Dette gøres
for at sikre en jævn arbejdsfordeling mellem de forskellige telefonistgrupper.
- SOF og TOF tager sig henholdsvis af de
funktioner, der er specifikke for de gratis tjenester og for de tjenester,
abonnenten betaler for.
Køprioritering.
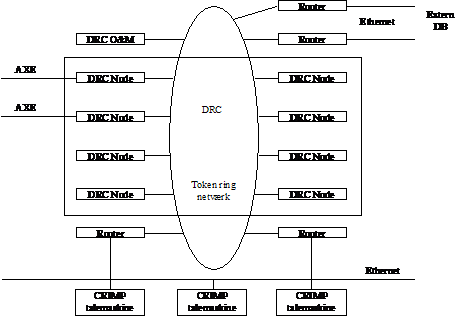
En af OPS vigtigste
opgaver er at fordele opgaverne til telefonisterne på en så retfærdig måde som
muligt. Disse telefonister sidder ved en WS, der er tilsluttet et token ring netværk i GLAD kaldet en
OTN-ring. Der er henholdsvis 16 og 12 OTN ringe øst og vest for Storebælt
placeret på geografisk forskellige steder, se Figur
3-11 hvor kddsa (vest) er
skitseret.
Telefonisterne
organiseres i grupper med et unikt navn. Disse grupper kan bestå af
telefonister, der er tilsluttet forskellige OTN ringe. Systemet kan håndtere op
til 128 telefonistgrupper, der defineres til at kunne håndtere bestemte typer
af opkald. Disse typer af opkald tildeles en prioritet fra 1-8 hvor prioritet 1
er højest, og disse prioriteter angiver i hvilken rækkefølge en bestemt gruppe
skal håndtere deres tildelinger. Det gælder dog her, at en kaldstype skal have
højeste prioritet mindst et sted, for at sikre at opkaldet bliver besvaret.
Prioriteten belyses i eksemplerne sidst i dette kapitel. Desuden kan der
tildeles kategorien ”direkte” til en kalds type, og disse prioriteter betyder
at telefonistgruppen straks vil håndtere indkomne kald af denne type. Dette
gælder f.eks. 112 opkald.
Som nævnt tidligere
er der for hver telefonistgruppe en a-værdi, der er et udtryk for hvor travlt
telefonisterne har
a-værdien skal forstås således, at tælleren angiver
hvor mange telefonister der er i gang med at betjene kunder, og nævneren er
antallet af bemandede pladser, der kan tage imod et opkald. a-værdien midles
over en ca. 5 minutters periode, og man får dermed en vægtet sum af forholdet
mellem afviklede opkald og antal mulige afviklede opkald, dvs. en slags
virkningsgrad for telefonistgruppen. a-værdien kan antage en værdi mellem 0 og 1,
hvor en stor værdi indikerer at den pågældende gruppe har lavet meget.
Når IN beder OPS om
at finde en telefonist, der kan betjene et opkald, finder OPS den
telefonistgruppe, der kan betjene den pågældende tjeneste og som har den
laveste a-værdi.
Måden OPS håndterer
disse informationer på belyses i det følgende med et par eksempler. I figurerne
herunder er vist et eksempel på fire telefonistgruppers a-værdier på et
givet tidspunkt, samt kaldstypernes prioritet og køstatus for tjenesterne.
|
|
|
|
|
|
Telefonist
gruppe 1
a1 = 0,95
|
118 prioritet = 1
TV prioritet = 2
144 prioritet = 3
|
|
Telefonist
gruppe 2
a2 = 0,99
|
TV prioritet = 1
118 prioritet = 2
144 prioritet = 3
|
|
Telefonist
gruppe 3
a3 = 0,90
|
144 prioritet = 1
TV prioritet = 2
118 prioritet = 3
|
|
Telefonist
gruppe 4
a4 = 0,85
|
144 prioritet = 1
TV prioritet = 2
|
|
|
|
|
|
|
|
Tjeneste
|
Kø status
|
|
118
|
ingen kø
|
|
144
|
kø
|
|
TV
|
kø
|
|
|
|
|
Figur 3-12 Prioriteringer i 4 telefonistgrupper.
|
Figur 3-13 kø situation for tre services.
|
Eksempel 1.
Der indkommer et
118 kald. OPS finder den gruppe, som har den laveste a-værdi samt kan
betjene et 118 kald og som har en ledig telefonist.
Da telefonistgruppe
3 har den mindste a-værdi af dem, der kan betjene et 118 kald, vælges
denne gruppe af OPS. Hvis der er flere ledige telefonister i denne gruppe,
vælges den telefonist, der har haft mindst at lave i et tidsinterval på 5 min.
Er der ikke nogen ledig telefonist fortsættes søgningen i gruppe 1, da denne
har den næsthøjeste a-værdi og kan betjene et 118 kald. Denne cyklus
fortsættes indtil der er fundet en ledig telefonist, eller kunden får en time
out.
Eksempel 2.
Der er kø for TV og
144 kald og OPS venter på en ledig telefonist Når en telefonist bliver ledig,
bliver hun tildelt det kald, som hun har højest prioritet til.
-
Hvis
der bliver en telefonist ledig i gruppe 4, bliver han/hun tilbudt et 144 kald.
-
Hvis
der bliver en ledig telefonist i gruppe 1 får han/hun et TV kald.
Som det ses i
eksempel 2, anvendes prioriteringen når der er kø. Hvis man ser på situationen
fra telefonistens side, så vil telefonisten i det øjeblik han/hun bliver ledig,
tildeles den tjeneste til hvilken han/hun har højeste prioritet. Dette burde
være medvirkende til at køer afvikles hurtigst muligt, hvis telefonisternes
prioritering af tjenesterne er relateret til hvor øvede de er i de respektive
tjenester.
AIP er et for AXE eksternt miljø, til håndtering og
bearbejdning/udførelse af instruktioner fra IN. AIP’en muliggør brugen af
eksterne audio tjenester og data behandling (non-audio). AIP består, som det
fremgår af Figur 3-1, af et antal CRIMP talemaskiner og DRC, som
distribuerer de enkelte funktioner. Distributionen sker via et netværk, hvor GW
(gate ways) til de enkelte ressourcer er placeret. DRC’en distribuerer
ressourcer såsom talemaskiner til AXE.
DRC platformen skal betragtes som et multi-node
system, der er i stand til at tilbyde et væld af ressourcer, det være sig
audio- og non-audio ressourcer. Konfigurationen af DRC er skitseret i Figur 3-14.
Hver DRC-node / GW kan være konfigureret til at
håndtere et eller flere ressourcer, som vist herunder.
- Adgang til AXE via GW med SS7 IPUP
signalering.
- Adgang til audio (CRIMP talemaskiner)
ressourcer.
- Adgang til non audio ressourcer, dvs. DB
ressourcer.
- Adgang til O&M (Operation & Maintenance)
ressourcer, anvendes til drift og vedligeholdelses operationer.
Det skal bemærkes at DB ressourcerne ikke anvendes i
GLAD systemet. Hvilken CRIMP, der er brugbar vælges af DRC og dette gøres udfra
til hvilken CRIMP der er ledig og hvilken besked, der skal gives.
For at begrænse dette projekts omfang, undersøges
som nævnt i kap.2
kun OP118 tjenesten. Derfor introduceres tjenesten kort i det følgende afsnit.
TDK har oprettet en service på nummeret 118, kaldet
oplysningen (OP118). Denne service har til formål at give kunder oplysninger om
andre abonnenters telefonnumre, navne og adresser. Til dette formål sidder der
telefonister flere forskellige steder i Danmark, der vha. en WS (work station)
kan søge efter information på en DB (Data Base).
Når en kunde kalder OP118 og der er en ledig
telefonist, oprettes der en taleforbindelse mellem kunden og telefonisten og en
dialog begynder. Hvis der ikke er en ledig telefonist sættes kunden i kø. Denne
kø kaldes Demand queue. Er denne kø ikke tilgængelig pga. at køen er fyldt op,
eller længste ventetid er overskredet, vil kunden blive stillet over til den
anden central (overløb), og dér vil kunden enten få straksbetjening eller blive
sat i en anden Demand queue, der er beregnet til overløb. Er denne også fyldt
op eller længste ventetid er overskredet, vil kunden blive nedkoblet.
Når kunden har fået en telefonist, og denne har
fundet de ønskede informationer, f.eks. et B-nummer, kan telefonisten enten
selv oplyse kunden om nummeret, eller stille kunden videre til audio release,
dvs. en talemaskine.
Det bliver indikeret på telefonistens WS, hvis der
ikke er en ledig talemaskine til audio release, og betjeningen fortsætter da
manuelt.
Manuel
betjening.
Ved manuel betjening kan telefonisten oprette en
forbindelse mellem kunden og B-abonnenten, manuel CC (call completion).
Audio
release.
Når kunden er stillet videre til en talemaskine, får
kunden først at vide hvad B-nummeret er: ”Nummeret er XXXXXXXX”, herefter får
kunden tre valg
- “Tast 1 for viderestilling til nummeret, det
koster xx kr.”
- “Tast 2 for gentagelse af nummeret”, ( dette
kan dog kun gøres to gange ).
- “Tast 3 for at blive stillet tilbage til en
telefonist” ( OFB ).
Hvis kunden ikke foretager sig noget i et bestemt
tidsinterval, eller forsøger at få gentaget nummeret mere end to gange, bliver
kunden stillet om til en telefonist. Hvis der ikke er en ledig telefonist,
sættes kunden i kø, denne kø kaldes Recall queue. Det samme gælder, hvis der
ikke er en telefonist ledig, når en kunde har valgt OFB.
Der findes tre forskellige kø systemer i OP118
tjenesten
- Demand queue med overløb.
- Demand queue uden overløb.
- Recall queue.
Demand
queue uden overløb.
Demand queue er en alm. forspørgselskø uden nogen
speciel prioritering, hvor afvikling af køen vil foregå efter FIFO (first in
first out) princippet. Kunder der ringer til de forskellige services, som her
OP118, vil blive sat i en demand queue, hvis der ikke er mulighed for
straksbesvarelse.
Når en kunde ankommer til en demand queue vil denne
få forskellige kømeldinger, som beskrives senere, uden at der er oprettet en
taleforbindelse til kunden. Kunden vil derfor ikke blive takseret i den tid
denne er i kø.
I det øjeblik kunden kommer i kontakt med en
telefonist, vil der så blive oprettet en taleforbindelse og takseringen vil
begynde. Hvis kunden befinder sig mere end 90 ± 30
sek. i køen vil kunden blive nedkoblet. Timeren, der styrer hvor længe en kunde
må befinde sig i køen, er en netovervågningstimer, der netop træder i kraft,
når der ikke er oprettet en taleforbindelse mellem centralen og kunden.
Hvis køen er fuld eller den længste ventetid, her 40
sek., er overskredet, vil kunden blive omstillet til den anden AXE central (se
næste afsnit).
Demand
queue med overløb.
Hvis demand queuen ikke er tilgængelig pga. at køen
er fuld, eller den længste ventetid i køen er overskredet, så har TDK for
nyligt (efteråret 97) indført et overløbssystem, der sender kunden over til den
anden AXE central. Her vil kunden blive anbragt i en ny demand queue, hvis
straksbetjening ikke er mulig Denne kø kaldes her Demand queue med overløb. Da
det er en demand queue gælder de samme regler som beskrevet i det forgående
afsnit, bortset fra, at hvis denne kø er fuld eller den længste ventetid i køen
(her 40 sek.) er overskredet, vil kunden blive nedkoblet og ikke sendt retur.
Recall
queue.
Recall queue er en forspørgselskø lige som Demand
queuen. Recall queue er dog behæftet med en prioritering der svarer til
prioriteringen for et 112 kald Prioriteringen for et 112 kald er dog højere.
Køen vil lige som Demand queue blive afviklet efter FIFO princippet.
Når en kunde ankommer til en Recall queue, vil
kunden få de samme kømeldinger som i Demand queue. Der er dog den forskel, at
kunden her vil blive takseret mens han/hun er i kø, da der på dette tidspunkt
er oprettet en taleforbindelse.
Hvis køen er fuld eller den længste ventetid i køen
er overskredet, vil kunden blive nedkoblet. Dette er dog usandsynligt pga. den
høje prioritering og pga. at TDK har bestemt, at en kunde ikke må befinde sig i
køen mere end ca. 4 sek.
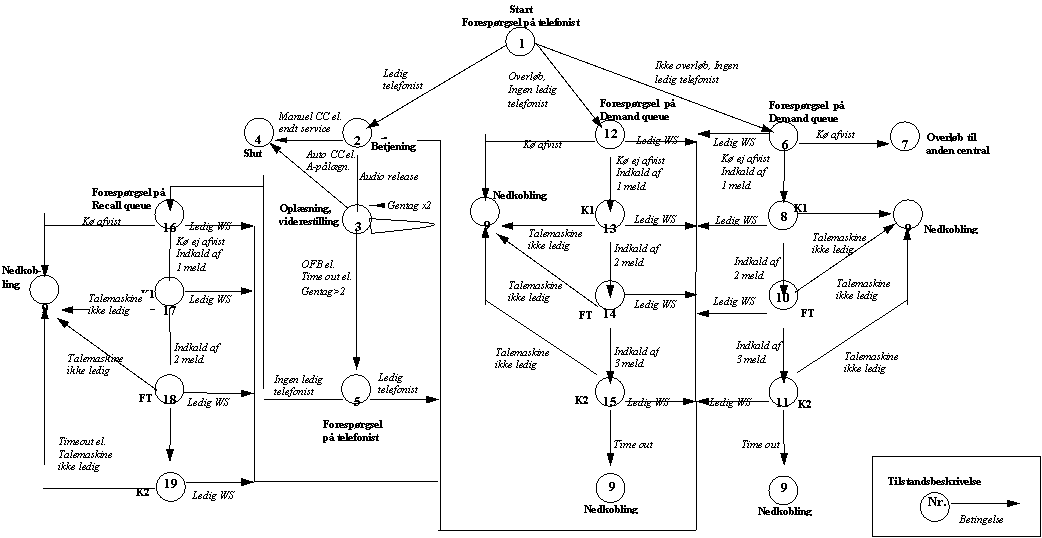
På basis af
interviews med {1} og {2} samt studering af [2] og [3], er der konstrueret et
tilstandsdiagram over OP118 servicen. Det skal her fremhæves, at dette
tilstandsdiagram kun beskriver ét kalds skæbne, og det kan derfor ikke bruges
til at bestemme “flowet” i OP118 tjenesten. Diagrammets anvendelse er da
primært at danne sig et detaljeret overblik over et kalds mulige skæbner i
OP118 tjenesten. Det kan bl.a. bruges til at vurdere hvilke hændelser, det kan
være interessante at foretage statistiske opmålinger af, samt hvordan disse
målinger kan realiseres i praksis. Denne problematik behandles i kap.4.
Beskrivelse
af de enkelte tilstande.
(1)
Start
tilstand, kunden har kaldt OP118 og er kommet igennem til kddsa eller khdsa AXE
centralen.
Hvis der findes en ledig telefonist vil kunden blive omstillet til denne,
tilstand (2), er dette ikke tilfældet vil kunden blive sat i kø alt efter om
det er et overløbskald, tilstand (12), eller ikke, tilstand (6).
(2)
Fra tilstand
(1)
Der er en ledig
telefonist, kunden får en velkomst meddelelse: ”Det er oplysningen”,
telefonisten kan selv optage et alternativ til denne meddelelse. Derefter
foregår der en dialog mellem kunden og telefonisten.
Fra tilstand (5)
Der er en ledig
telefonist til at betjene OFB. Det skal bemærkes at denne rutine kan foretages
op til 255 gange. Derudover kan det være en kunden der ikke har reageret på
audio release, eller der er sket en time out i tilstand (3) eller der er
forsøgt at få gentaget nummeret mere end 2 gange, og der fortages derfor en
viderestilling til en ledig telefonist.
Fra Demand queue
Når en kunde
befinder sig i Demand queue vil den kunde der har befundet sig længst i køen
blive omstillet til en telefonist når denne er ledig. Dette vil ske uafhængig
af den tilstand kunden befinder sig i.
Fra Recall queue
Her gælder det
samme som i Demand queue. Der er dog forskel på prioriteringen af de to køer.
Recall queue tildeles en høj prioritet, normalt sådan at den kun kan overhales
af ankommende opkald til 112.
Der er fra tilstand (2) mulighed for manuel CC, audio release eller der kan
nedkobles efter endt betjening, som f.eks. ved oplysning af en adresse.
(3)
Der er valgt audio release fra tilstand (2), og kunden stilles om til
en talemaskine som læser nummeret op. Ved tryk på ”2” kan nummeret gentages,
dog max 2 gange. Forsøges det at gentage nummeret flere gange vil der ske en
omstilling til en telefonist tilstand (2), er en sådan ikke ledig vil kunden
blive sat i Recall queue tilstand (16). Forespørgsel om en ledig telefonist,
forgår i tilstand (5). Udover at gentage nummeret kan der fortages OFB eller CC
ved at taste henholdsvis ”3” eller ”1”.
(4)
Fra tilstand
(2)
CC er fortaget manuelt af
telefonisten tilstand (2), A-abonnenten stilles igennem
til B-bonnenten. Der kan også være fortaget en
nedkobling efter endt betjening, som f.eks. ved oplysning af en adresse.
Fra tilstand (3)
Kunden har tastet
”1” på telefonen og dermed valgt auto CC, A-abonnenten stilles igennem til B-abonnenten. Eller kunden har
efter at have hørt nummeret afbrudt forbindelsen.
(5)
Kunden har tastet ”3” og valgt Operator Fall Back, OFB, eller der er
forsøgt at få gentaget nummeret mere end 2 gange eller der er sket en time out
fra tilstand (3). Er en telefonist ledig vil der blive omstillet til denne,
tilstand (2), er dette ikke tilfældet sættes kunden i kø, tilstand (16).
(6)
Ingen overløb, og der er ingen ledig telefonist. Det undersøges om der
ikke er plads i køen og/eller længste ventetid overskrider 40 sek., er dette
tilfældet vil kunden blive omstille til den anden central, tilstand (7). Er der
ledig plads i køen vil kunden få den første meddelelse, tilstand (8).
(7)
Køen blev afvist, overløb til den anden centrals tilstand (1). Ved kø på den nye central sættes kunden
i en demand queue, tilstand (12), som svare til den almindelige demand queue,
tilstand (6) Disse to køer afvikles med samme prioritet.
(8)
Køen blev ikke afvist og der er ingen ledig telefonist, så første
melding (K1) afspilles: ”Velkommen til oplysningen, vi er desværre optaget,
vent et øjeblik. Ventetiden er gratis”.
(9)
Hvis der ikke er en ledig talemaskine i tilstandene (8), (10), (11), (13),
(14), (15), (17), (18) og (19) vil forbindelsen blive nedkoblet.
Der vil fortages en nedkobling ved kø afvist fra tilstand (12) og (16) og Time
out fra tilstand (11), (15) og (19). Nedkobling
(linienedkobling se kap. 3.3
eller kap. 3.8.1)
pga. Timeout foretages efter 90 ± 30 sekunder.
(10) Der er ingen ledig telefonist,
melding 2 (FT) afspilles: ”De er stadig i kø, forventet ventetid xx” (xx er
modulus 5 sek.).
(11) Stadig ingen ledig telefonist,
melding 3 (K2) afspilles: ”musik”.
Ved ophold i køen mere end 90 ± 30 sek. vil der ske en Time out
(linienedkobling se kap. 3.3
eller kap. 3.8.1) og kunden vil blive nedkoblet, tilstand (9).
(12) Overløb, og der er ingen ledig
telefonist. Det undersøges om der ikke er plads i køen og/eller længste
ventetid overskrider 40 sek., er dette tilfældet vil kunden blive nedkoblet,
tilstand (9). Er der ledig plads i køen vil kunden få den første meddelelse,
tilstand (13).
(13) Som tilstand (8).
(14) Som Tilstand (10).
(15) Som tilstand (11).
(16) Der er ingen ledig telefonist,
fra tilstand (5), og kunden placeres i Recall queue. Det undersøges om der ikke
er plads i køen og/eller længste ventetid overskrider 40 sek., er dette
tilfældet vil kunden blive nedkoblet, tilstand (9). Er der ledig plads i køen
vil kunden få den første meddelelse, tilstand (17). Under normale
omstændigheder vil kunden højst befinde sig i køen i ca. 4 sekunder, dette
skyldes den høje prioritering.
(17) Som tilstand (8)
(18) Som Tilstand (10).
(19) Som tilstand (11) bortset fra at
Time out er en separat tæller se kap. 3.8.1.
VIGTIG.
A-abonnenten
kan lægge på i alle tilstande og på den måde forårsage en nedkobling Disse
tilstandsskift er ikke medtaget i tilstandsdiagrammet.
I
dette afsnit vil det på grundlag af tilstandsdiagrammet over OP118 tjenesten
kap.3.9 blive
vurderet hvilke statistiske oplysninger, det vil være interessante at kende.
Disse vurderinger bliver sammenlignet med de faktiske statistiske data som TDK
anvender. Anvendelsen kan bl.a. være at se, om TDK’s kvalitetsmålsætning for
OP118 tjenestens fremkommelighed og svartid er opfyldt. Disse krav er vedlagt i
Bilag 1.
Der
vil først blive udarbejdet en vurdering af hvilke statistiske oplysninger, der
er relevante. Relevansen af disse oplysninger er afhængig af, hvad statistikken
skal anvendes til. Denne vurdering vil derefter blive holdt op mod den
statistik TDK på nuværende tidspunkt optager. Konklusionen på denne
sammenligning kan ende med et eller flere forslag til ændring af den nuværende
statistikopsamling.
Den
mest udførlige beskrivelse af systemet opnås ved opsamling af data i samtlige
tilstande. Dette vil dog hurtigt blive både dyrt og uoverskueligt. Derudover
vil der ske en unødvendig overbelastning af nettet pga. de store mængder af
data, der skal sendes til databanken.
Der
vil i projektet blive forsøgt at begrænse mængden af opsamlet data. Derfor
medtages kun de målinger, der skønnes nødvendige, for at kunne bestemme
fremkommelighed og svartid samt andre størrelser, der vurderes særligt
interessante.
Der
fortages i dag mange opkald til servicetelefonen, hvoraf de fleste er til
oplysningen. I dette projekt er det netop denne service, der arbejdes med.
Det
er selvfølgelig i TDK’s interesse, at afviklingen af denne trafik sker med en
så stor effektivitet som muligt. Ordet effektivt skal ses både fra forbrugerens
side, der selvfølgelig forventer en hurtig og problemfri service, og fra TDK’s
side, der både ønsker at tilfredsstille kundens behov, men samtidig ønsker at
omkostningsniveauet bliver holdt nede.
Omkostningsniveauet
og servicen er her styret af, hvor mange telefonister der er på arbejde, samt
hvor stort selve systemet er dimensioneret. Den væsentlige faktor er her
telefonisterne, da antallet af disse hele tiden kan varieres, hvorimod systemet
umiddelbart er sværere at ændre på. Problemet er så at vide, hvor mange
telefonister der skal være til stede på et vilkårligt tidspunkt.
Denne
problematik er netop en af de væsentlige, da antallet af kunder, der ringer op
til oplysningen, varierer meget. TDK løser dette problem vha.
statistikmålinger, som de bruger til at kunne forudse visse tendenser i
trafikken. Såsom
- Døgnrytme, hvor man ser på variationer i et
døgn, der typisk opdeles i timeintervaller.
- Årsrytme, hvor man ser på variationer i
løbet af året.
Ud
fra disse tendenser bestemmes så antallet af nødvendige telefonister i løbet af
et døgn og i løbet af året. TDK bruger også disse målinger til at holde op mod
deres målsætning (se Bilag 1), for at se om de lever op til de fastsatte krav.
Er dette ikke tilfældet, skal der selvfølgelig fortages en justering.
Pga.
teletrafikkens stokastiske natur vil en måling svare til en stikprøve af en
eller flere stokastiske variabler. Hvis man gentager en måling, kan man derfor
forvente, at man måler en anden værdi. Derfor vil man, som tidligere nævnt, kun
være i stand til at bestemme tendensen, dvs. sandsynligheden for at en værdi
ligger i et bestemt interval. Til praktiske formål, såsom statistik indsamling,
vil det være tilstrækkeligt at kende fordelingens middelværdi og varians,
fordelingstypen er dermed irrelevant (se kap.4.4.1).
For
at få det størst mulige udbytte og den størst mulige mængde af information,
skal arten af målingerne og de størrelser, der skal måles, vælges i
overensstemmelse med de krav der stilles.
Et
eksempel kan være at TDK ønsker at vide, hvor mange opkald de besvarer i OP118.
Her er det ikke nok at vide, hvor mange opkald, der er fortaget til
oplysningen. De skal også vide, hvor mange der ikke har fået den forventede
betjening. En manglende betjening kan være forårsaget af, at kunden har lagt
på, eller af en nedkobling fra TDK’s side. Denne nedkobling kan skyldes
overbelastning, mangel på talemaskiner eller lignende. Ved at sammenholde disse
målinger med hinanden vil TDK kunne få oplyst hvor mange opkald de har betjent.
Men de vil også ved at tage den procentvise forskel mellem de to tal, kunne få
en værdi for, hvor mange kunder de har betjent i forhold til dem, der har
ringet.
Hvad
der er relevant at måle og hvad der bliver målt vil blive behandlet i kap.4.3 og kap.4.6.
Der vil i dette afsnit blive fremlagt hvilken
statistik der menes relevant, samt en begrundelse derpå.
Inden det vurderes, hvilken statistik der
skal opsamles, er det vigtigt at gøre sig klart hvad den skal bruges til. Man
kan her dele anvendelsen op i to kategorier
- Effektivitet, der er et udtryk for hvor godt
den ankomne trafik afvikles.
- Problemlokalisering, hvor det vha. statistik
skulle være muligt, at finde de steder i systemet, hvor trafikken ikke afvikles
efter forventning.
Der er her valgt at måle følgende
størrelser, som beskrives i de næste afsnit.
- Besvarelsesprocent.
- Betjeningstid.
- Nedkoblingsprocent.
- Kønedkoblingsprocent.
- Køtid.
- Kø-afvist.
Besvarelsesprocent.
Den nemmeste måde at finde et udtryk for
systemets effektivitet ville være at finde besvarelsesprocenten.
Besvarelsesprocenten defineres på følgende måde
Hvor ”Antal besvarede opkald” er det antal
opkald telefonisterne besvarer, og ”Antal samlede opkald” er det antal opkald,
der samlet ankommer til OP118. Det skal her nævnes, at opkald der afvises
udenfor GLAD systemet, dvs. i PSTN netværket, ikke medtages i ”Antal samlede
opkald”, da dette projekt ikke omfatter en total vurdering af TDK’s netværk.
Besvarelsesprocenten er derfor et direkte
udtryk for, hvor mange af de ankommende kald der bliver besvaret af
telefonisten, og er det samme som TDK’s fremkommelighed i bilag 1.
Det optimale ville være en
besvarelsesprocent på 100%, men TDK’s krav er at besvarelsesprocenten mindst
skal være 95% i hverdagene.
Visse hændelser kan virke forstyrrende på
besvarelsesprocenten.
1. Hvis en kunde under audio release vælger OFB
eller får en time out, vil denne kunde blive betjent endnu engang. Dvs. at
kunden vil blive registeret to gange i ”Antal besvarede opkald”, og kun en gang
i ”Antal samlede opkald”. Besvarelsesprocenten bliver hermed for stor, og kan i
særlige tilfælde blive over 100%, hvilket ikke giver nogen mening.
2. Hvis A-abonnenten afslutter opkaldet inden
betjening, vil dette bevirke en forringelse af Besvarelsesprocenten.
Da disse to forstyrrelser har modsat
indvirkning på Besvarelsesprocenten, er det ikke muligt at vide hvilken
indflydelse de samlet har på Besvarelsesprocenten. Man kan dog sige at
størrelsen af forstyrrelsernes indvirkning på besvarelsesprocenten er afhængige
af antallet af disse hændelser set i forhold til det samlede antal opkald til
OP118.
Det vil være relevant at måle
Besvarelsesprocenten for hele systemet og for de enkelte telefonistgrupper, for
at få et overblik over hvor effektive de enkelte telefonistgrupper er i forhold
til hinanden og i forhold til hele systemet.
Betjeningstid.
En tid, det kunne være relevant at måle
ville være den tid en telefonist er om at betjene en kunde Denne tid kaldes
betjeningstiden. Betjeningstiden vil kunne bruges til at kontrollere, hvor
hurtigt de enkelte kunder bliver betjent og dermed også hvor effektivt.
Betjeningstiden defineres på følgende måde.
|
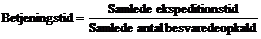
|
( 4-2)
|
Hvor den ”samlede
ekspeditionstid” er summen af de enkelte ekspeditionstider.
En væsentlig faktor, der vil
have indflydelse på betjeningstiden, er den prioritering de forskellige services
har (se kap.3.6).
Ved opkald, der har en høj prioritering må det formodes, at betjeningstiden vil
være kort, da telefonisten for det meste kun besvarer disse opkald og dermed
får en vis rutine, hvorimod lavprioriterede opkald vil have en længere
betjeningstid. For at vurdere betjeningstiden er følgende nødvendigt at vide.
- Gennemsnitlige betjeningstid for alle TDK’s
telefonistgrupper. Målingen vil kunne bruges til sammenligning med andre
televirksomheders OP118 tjenester (hvis disse informationer er tilgængelige),
og ud fra dette vurdere om servicetelefonen er konkurrencedygtig.
- Betjeningstiden for de enkelte
telefonistgrupper. Ved at sammenholde denne værdi med den gennemsnitlige
betjeningstid, vil de telefonistgrupper hvis betjeningstid ligger langt over
landsgennemsnittet kunne udpeges.
- Betjeningstiden for den enkelte telefonist.
Her vil der være mulighed for at kontrollere, hvor effektiv den enkelte
telefonist er, både i forhold til telefonistgruppen og til de andre telefonister.
Det vil kun være nødvendigt at kontrollere
betjeningstiden for henholdsvis telefonistgrupperne og telefonisterne hvis den
gennemsnitlige betjeningstid vurderes at være for lang.
Nedkoblingsprocent.
Nedkoblingsprocenten er den del af kunderne,
der nedkobles i køerne i forhold til det samlede antal kunder, der nedkobles i
systemet. Det skal bemærkes, at der her er valgt at betragte de tre køtyper
(Recall queue og de to Demand queues se kap 3.8.1)
samlet, da en teknisk fejl, f.eks. en defekt talemaskine, vurderes at have
samme indflydelse på de tre køer.
Nedkoblingsprocenten defineres på følgende
måde
Når man betragter Besvarelsesprocenten vil
denne blive dårligere jo flere kunder der nedkobles. Ved en for lav
Besvarelsesprocent, kan man, ved hjælp af nedkoblingsprocenten, finde ud af,
hvor den største nedkobling foregår.
Af formel (
4-3) ses, at Nedkoblingsprocenten er ”Antal nedkoblet i køerne” i forhold
til ”Total antal nedkoblet”. Det betyder, at de samlede antal nedkoblinger
deles op i to områder, nedkobling i køerne og nedkobling udenfor køerne.
- Det vurderes, at de nedkoblinger der foregår
uden for køerne hovedsagelig skyldes tekniske problemer eller at kunden
afbryder forbindelsen, enten fordi de fortryder opkaldet, eller fordi de ikke
vil være i kø.
- Nedkobling i køerne skyldes pålægning fra
abonnents side pga. utålmodighed eller nedkobling fra TDK’s side. Kunder der
mister tålmodigheden i køen er et udtryk for en dårlig afvikling af køen, mens
nedkoblinger fra TDK kan være forårsaget af f.eks. tekniske problemer.
Ved en Nedkoblingsprocent støre end 50% vil
størstedelen af nedkoblingerne foregå i køerne, og det vil derfor være
hensigtsmæssig at lave en forbedring i køerne. Forbedringen vil være stærkt
afhængig af om nedkoblingerne skyldes nedkoblinger fra TDK’s side, eller
pålægning fra kundens side. Dette vil blive udspecificeret i afsnittet om Kønedkoblingsprocent.
Antager Nedkoblingsprocenten en værdi mindre
end 50%, vil størstedelen af nedkoblingerne foregå uden for køerne. Her vil det
kun være de tekniske problemer som TDK kan tage sig af, da det antal kunder,
der nedkobler forbindelsen inden de får betjening, eller kommer i kø, ikke er
noget TDK har indflydelse på.
Kønedkoblingsprocent.
Kønedkoblingsprocenten er udtrykt ved den
del af kunder, der nedkobles i køerne i forhold til de samlede antal kunder,
der ankommer i køerne. Denne udregning kan bruges, hvis det ud fra
Nedkoblingsprocenten er påvist, at det hovedsagelig er nedkobling i køerne der
er årsag til den eventuelle lave Besvarelsesprocent.
Kønedkoblingsprocenten defineres på følgende
måde.
|
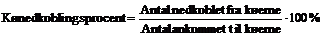
|
( 4-4 )
|
Som for Nedkoblingsprocenten må gælde, at jo
højere Kønedkoblingsprocent, des lavere Besvarelsesprocent. Ved at betragte
Kønedkoblingsprocenten ud fra tre synsvinkler, vil man mere specifikt kunne
konkludere, hvad der er årsagen til den lavere Besvarelsesprocent.
- Hvor ”Antal nedkoblet fra køen” er det
samlede antal kunder, der nedkobles.
- Hvor ”Antal nedkoblet fra køen” er det antal
af kunder, der selv afbryder forbindelsen.
- Hvor ”Antal nedkoblet fra køen” er det antal
af kunder, der nedkobles af TDK.
Man kunne vælge at se på det samlede antal
kunder, der enten nedkobles eller afbryder forbindelsen selv, til hurtigt at få
et overblik over, hvor godt køerne afvikles.
Ved at betragte nedkoblinger forårsaget af
TDK, og afbrydelser forårsaget af kunden separat, vil man kunne se hvilken af
disse to, der er den væsentlige faktor. Drejer det sig om TDK nedkoblinger, vil
det være en decideret fejl såsom defekte eller for få talemaskiner, Time out
eller kø-afvist (for Time out eller kø-afvist se kap.3.8). Hvis det derimod drejer sig om
pålægninger, når en kunde f.eks. møder en kømelding, er det en faktor som er
svær at gøre noget ved. Derimod er det antal kunder, der afbryder forbindelsen
pga. utålmodighed, et udtryk for en dårlig afvikling af køen. En dårlig
afvikling af køen vil vise sig ved at den gennemsnitlige ventetid i køerne er
for lang.
Køtid.
I afsnittet om Kønedkoblingsprocent er det
nævnt at nedkoblinger forårsaget af TDK skyldes defekte eller for få
talemaskiner, Time out eller kø-afvist.
- Time out, er en nedkobling, der foretages
efter en kunde har befundet sig i køen længere tid end et på forhånd fastsat
tidsrum, se kap. 3.8.
- Kø-afvist, er en nedkobling, der foretages
hvis en kunde ”forspørger” om en plads i køen og den længste ventetid er over
et på forhånd fastsat niveau eller køen er fyldt op, se kap.3.8.
Som det ses er både Time out og til dels
Kø-afvist tidsafhængige. Ved at definere Køtid som den tid der går fra en kunde
ankommer i køen til kunden omstilles til en ledig telefonist, vil det være
muligt at se om nedkoblingerne skyldes en for dårlig afvikling af køen, hvilket
vil sige at for mange kunder får en nedkobling pga. en time out eller kundens
tålmodighed er sluppet op. En for dårlig afvikling af køen skyldes at der er
for få telefonister til at servicere kunderne.
Det er dog et problem, at Kø-afvist også kan
skyldes for mange kunder i kø.
Kø-afvist.
Hvis problemet med nedkoblinger ikke skyldes
en for dårlig afvikling af køen (se Køtid), kan det være problemer med
talemaskinerne eller en for lille kø. For at kunne få en ide om, hvor mange
nedkoblinger der skyldes en for lille kø, skal Kø-afvist måles, der er det antal kunder, der afvises inden de kommer i
kø. Denne værdi indbefatter også de kunder der afvises pga. at køens længste
ventetid er for lang, men hvis Køtid ikke er for stor i forhold til den
fastsatte længste ventetid ( for længste ventetid se kap.3.8 ), har dette ingen
betydning. Man kan så ved at sammenholde Kø-afvist med køtid kontrollere om Kø-afvist hovedsagelig skyldes
kø-fuld eller for lang ventetid. Hvis kø-afvist er stor i forhold til det antal
kunder der nedkobles i køerne, betyder dette en dårlig afvikling af køerne, og
ikke en teknisk fejl.
Generelt.
For at den indsamlede data kan bruges til at
vurdere, hvor mange telefonister, der skal være på arbejde i løbet af døgnet og
året, skal statistikken opsamles i nogle intervaller. Intervallerne skal give
TDK en ide om, hvor belastet systemet er på forskellige tidspunkter, dvs. hvor
mange kunder, der ringer ind til oplysningen. Derudover skal TDK også kunne se
om de lever op til de fastsatte krav i intervallerne, som de kan bruge til at
se om der er for få eller for mange telefonister på arbejde.
Et eksempel på dette kunne være
- Timeinterval, for at få en rimelig
detaljeret oversigt af døgnet.
- Daginterval, for at få en ide om hvilke dage
om året, der er mest belastet.
- Uge interval, for at se hvordan trafikken er
fordelt på en uge.
- Månedsinterval, for at se fordelingen af
trafikken i løbet at året
- Årsinterval, for at se om der er stigende
eller faldende interesse for netop denne service.
Udover at målingerne skal fortages for den
enkelte telefonist og telefonistgruppe og endelig for hele systemet, ville en opdeling af Danmark i øst og vest også være
hensigtsmæssig, da det er de områder de to centraler hver især dækker.
Der
vil i dette kapitel blive vurderet hvordan de i kap.4.3 ønskede værdier kan måles. Vurderingen af
hvilke målinger der skal foretages vil blive gjort ud fra tilstandsdiagrammet i
kap.3.9. Derudover vil der også blive givet simple
forslag til hvilke målemetoder der evt. kunne være relevante at anvende.
Da
de i kap.4.3
ønskede værdier skal udregnes ud fra en eller flere stokastiske variable, vil
man ved gentagelse af en måling ikke kunne forvente at få den samme værdi, men
man vil kunne sige at den ubekendte værdi med en vis sandsynlighed ligger i et
bestemt interval. Man er derfor kun i stand til at bestemme en tendens. Til
praktiske formål er det som regel nok at kende middelværdien og variansen, det
er derfor ikke nødvendigt at kende fordelingstypen.
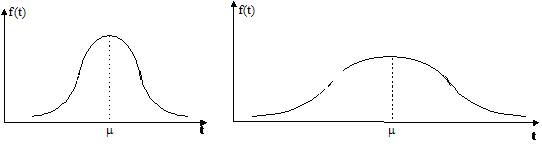
Hvorfor
det er nødvendigt at kende variansen kan forklares ved at betragte Figur 4-1 og
Figur 4-2
der er en skitse over to forskellige fordelinger af f(t) over f.eks. ventetiden t.
Figurerne viser henholdsvis en “smal” fordeling og en “bred” fordeling dvs. en
fordeling med henholdsvis en lille og en stor varians, s2. Fordelingerne har begge middelværdien m.
Da fordelingsfunktionen
på Figur 4-1
har en lille varians vil sandsynligheden for at en vilkårlig ventetid ligger
tæt på middelværdien, være større end hvis variansen var stor, som på Figur 4-2.
Det er netop derfor, at det er nødvendigt at kende variansen, da man ikke alene
ud fra middelværdien kan få en ide om ventetidsfordelingen, hvis variansen er
stor.
Til
måling af data findes flere klassiske målemetoder, hvoraf to nævnes her.
-
Kontinuert måling, hvor
målepunktet er aktivt, hvilket vil sige at en hændelse vil blive registreret i
det øjeblik den indtræffer.
-
Skannemetoden, hvor alle hændelse
der indtræffer mellem to skannetidspunkter registreres. Derefter henstilles
målingen tidsmæssigt til det sidste skannetidspunkt. Dette gøres med bestemte
intervaller.
Den
kontinuerte målemetode er den mest præcise af de to metoder, men også den
metode der kræver den største lagerplads, da alle hændelser bliver registreret.
Denne metode, vil være relevant at bruge i tilfælde hvor man skal bruge eksakte
værdier for f.eks. en ankommen trafik.
Skannemetoden
bruges steder hvor der ønskes sparet på lagerpladsen. Ulempen ved skannemetoden
er at den ikke er eksakt, men ved at vælge størrelsen af intervallerne rigtig
vil man kunne få gode tilnærmede værdier for de virkelige hændelser. En sådan
måling kunne bruges på steder hvor trafikken er regelmæssig dvs. forholdsvis
jævnt fordelt. Hvilken metode der kan anvendes til måling af de ønskede værdier
nævnes i de tilhørende afsnit i kap 4.4.2.
En
beskrivelse af de tekniske muligheder for hvad der kan måles, eller hvorledes
målingerne gennemføres er der ikke mulighed for at beskrive nærmere i dette
projekt, da det ville blive for omfangsrigt i forhold til den afsatte tid. Der
kan derfor opstå problemer med at TDK ikke kan foretage de målinger der
forlanges og det må derfor af TDK vurderes om der tilnærmelsesvis kan findes en
tilsvarende måling. Hvordan målinger skulle kunne fortages, kunne måske uddybes
i et senere projekt.
Der
vil til hver af de ønskede værdier i kap.4.3
blive bestemt hvilke målinger der skal fortages for at disse kan beregnes, samt
forslag til en målemetode. Derefter vil alle målingerne blive samlet og evt.
dobbeltmålinger fjernet. Vurderingen af hvilke målinger der skal fortages, vil
blive gjort ud fra tilstandsdiagrammet over OP118 (se kap.3.9). Det skal dog
pointeres, at diagrammet ikke er et flow diagram men et situationsdiagram. Det
er derfor ikke muligt at fortage de nødvendige målinger ud fra
tilstandsdiagrammet, men kun at bestemme hvilke målinger der skal fortages.
Generelt
for alle målinger gælder, at disse skal lagers for hver time, døgn, uge og
måned for at få et detaljeret overblik over de variationer der opstår i løbet
af disse intervaller. Man vil ud fra dette kunne bestemme visse tendenser i
trafikken og dermed kunne få en ide om antallet af nødvendig telefonister.
Derudover
skal målingerne deles op i henholdsvis øst og vest dvs. målinger fra kddsa og
khdsa, samt deles op i de enkelte telefonistgrupper og telefonister. Dette skal
gøres for at have mulighed for at sammenligne de enkelte delsystemer og
telefonister med hinanden og dermed kunne udpege de svage punkter, for derefter
evt. at lave en effektivisering at disse.
Der
vil i dette kapitel blive vurderet hvilke målinger der skal foretages samt
hvilken metode der kan anvendes til måling af de ønskede værdier.
Disse
målinger består i at bestemme antal hændelser n i et bestemt tidsinterval. Forskellige typer af hændelsesantal
der anvendes til samme beregning, skal være målt i det samme tidsinterval.
Besvarelsesprocent.
Besvarelsesprocenten
er defineret som ”Antal besvarede opkald” i forhold til ”Antal samlede opkald”.
OFB eller abonnent pålægninger vil her
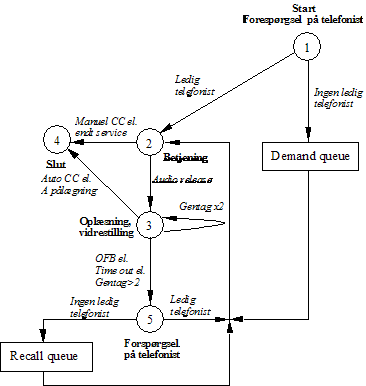
kunne være årsag til en fejl i beregning af Besvarelsesprocenten (se kap.4.3). For at få et
overblik over hvordan de forskellige faktorer indvirker på
Besvarelsesprocenten, er der ud fra Figur
3-15 lavet et forenklet udsnit af OP118 diagrammet (se Figur 4-3).
|
|
|
Figur 4-3 Simplificeret
udgave af OP118 tilstandsdiagram.
|
Ved
at betragte Figur
4-3 kan man se at problemet med “OFB” kunne løses ved at ”Antal
besvarede opkald” er det antal kunder der forlader systemet efter endt
betjening, samt de kunder der vælger OFB, får en time out eller de kunder der
har fået gentaget nummeret mere end to gange.
For
at besvarelses procenten ikke skal blive over 100% skal følgende hændelser
inkluderes i ”Antal samlede opkald”.
- kunder der vælger OFB.
- kunder der får en time out.
- kunder der har fået gentaget nummeret mere
end to gange.
Problemet
med abonnent pålægninger er en lidt mere kompleks. Problemet består i først at
vurdere om pålægningerne er en fejlfaktor for besvarelsesprocenten, og derefter
hvis dette er tilfældet, hvor stor en del af pålægningerne der skal tages med.
Det vurderes her at pålægningerne er et problem, dermed menes at de er et
udtryk for en for dårlig afvikling af kunderne, men det er kun de pålægninger
der foregår i køerne og ikke de kunder der fortryder inden de får en telefonist
dvs. ved ankomstmeldingen eller de kunder der afbryder forbindelsen ved første
kømelding. Denne vurdering tages på grundlag af, at folks reaktion på at bliver
sat i kø, eller at opkaldet fortrydes kan betyde en pålægning fra kundens side,
ikke er noget TDK umiddelbart kan gøre noget ved. For at disse værdier ikke får
en negativ indflydelse på Besvarelsesprocenten skal de medregnes i ”Antal
besvarede opkald”. Det antal kunder der foretager en pålægning mens de er i kø
må betragtes som et udtryk for at systemet ikke fungere korrekt, og dermed
bevirker en dårligere besvarelsesprocent.
Der
skal fortages følgende målinger for at kunne bestemme ”Antal besvarede opkald”.
n1 = Manuel
CC, der udføres af telefonisten.
n2 = Auto
CC, der udføres af abonnenten.
n3 = Endt
service, hvor telefonisten selv oplyser det ønskede og derefter nedkobler
forbindelsen.
n4 = Abonnent
pålægning, hvor kunden selv fortage en pålægning efter endt oplæsning af
telefonnummer.
n5 = Abonnent
pålægning, hvor kunden har fortaget en pålægning før betjening.
n6 = Abonnent
pålægning, hvor kunden har fortaget en pålægning inden eller under første
kømelding i Demand queue.
n7
= OFB, Time out eller gentagelse af nummeret
er sket mere end to gange.
”Antal
besvarede opkald” = n1 + n2 + n3 + n4
+ n5 + n6 + n7
Der
skal fortages følgende målinger for at kunne bestemme ”Antal samlede opkald”.
n8 = Antal opkald til OP118.
n7 = OFB,
Time out eller gentagelse af nummeret er sket mere end to gange.
”Antal
samlede opkald” = n7 + n8
|
Besvarelsesprocent = 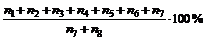
|
( 4-5 )
|
Da
Besvarelsesprocenten er en rimelig betydende værdi for systemets effektivitet
og da det også er den værdi der bruges til at fastsætte TDK’s målsætningen vil
det være den kontinuerte målemetode der skal anvendes her.
Betjeningstid.
Betjeningstiden
er defineret som ”Samlede ekspeditionstid” i forhold til ”Samlede antal
besvarede opkald”. Dette gøres for at få en middelværdi som kan bruges til
sammenligning af de enkelte telefonister/telefonistgrupper.
Den
samlede ekspeditionstid er en akkumulering af de enkelte tider, det tager en
telefonist at betjene en kunde. ”Samlede antal besvarede opkald” er det antal
opkald telefonisten besvarer inkl. de opkald der kommer fra OFB, Time out eller
gentagelse af nummeret er sket mere end to gange.
Der
skal derfor fortages følgende målinger.
n9 = Den
samlede tid det tager at betjene kunderne (Bemærk at n9 er en tid, og ikke et antal hændelser).
n1 = Manuel
CC, der udføres af telefonisten.
n2 = Auto
CC, der udføres af abonnenten.
n3 = Endt
service, hvor telefonisten selv oplyser det ønskede og derefter nedkobler
forbindelsen.
n4 = Abonnent
pålægning, hvor kunden selv fortage en pålægning efter endt oplæsning af
telefonnummer.
n7
= OFB, Time out eller gentagelse af nummeret
er sket mere end to gange.
|
Betjeningstid = 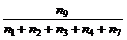
|
( 4-6 )
|
Da
det vurderes at Betjeningstiden er rimelig relevant til bestemmelse af hvor
effektive telefonisterne/telefonistgrupperne er, vil det være den kontinuerte
målemetode der skal anvendes her. Ved mangel på lagerplads, eller hvis det
vurderes at transmissionen af den store mængde data vil belaste systemet for
meget, vil man også kunne anvende skanne metoden.
Nedkoblingsprocent.
Nedkoblingsprocenten
er defineret som ”Antal nedkoblet i køerne” i forhold til ”Antal total
nedkoblet”. Antal nedkoblet i køerne er det samlede antal der nedkobles i de
tre køtyper (se kap.4.3).
For at bestemme antallet af kunder der nedkobles i køerne skal følgende måles.
n10 = Kø
afvist, der er det antal der afvises pga. kø-fuld eller ventetiden er for lang.
n11 = Talemaskine
ikke ledig, er det antal kunder der afvises pga. for få eller defekte
talemaskiner i køerne. Abonnent pålægning i køerne.
n12 = Time
out, der er det antal kunder der afvises i køerne fordi ventetiden var for
lang.
Antal
nedkoblet i køerne = n10 +
n11 + n12
For
at bestemme antallet af de kunder der nedkobles totalt i systemet skal følgende
måles.
n10 = som beskrevet overfor.
n11 = som beskrevet overfor.
n12 = som
beskrevet overfor.
n13
= Abonnent pålægning total.
Antal
total nedkoblet = n10 + n11 + n12 + n13
|
Nedkoblingsprocent = 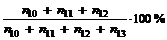
|
( 4-7 )
|
For
at få de mest nøjagtige tal vil det være den kontinuerte målemetode der skal
anvendes her, men man vil også kunne anvende skanne metoden. For at bruge
skanne metoden skal intervallerne dog være så små, at man ikke mister vigtige
data pga. døgnrytmen.
Kønedkoblingsprocent.
Kønedkoblingsprocenten
er defineret som ”Antal nedkoblet fra køerne” i forhold til ”Antal ankommet til
køerne”.
Der
er i kap.4.3 lagt
op til at det antal der nedkobles i køerne, kan deles op i det antal af
abonnenter der selv nedkobler forbindelse og de nedkoblinger der er forårsaget
af TDK. Der skal tages følgende målinger.
Antal
nedkoblet i køerne forårsaget af TDK.
n10
= Kø afvist, der både kan bevirke nedkobling
eller overløb.
n12
= Time out, der er det antal kunder der
afvises i køerne fordi ventetiden var for lang.
n14
= Talemaskine ikke ledig, der er de
nedkoblinger ASTDR talemaskinerne forårsager.
Antal
nedkoblet fra køerne forårsaget af TDK = n10
+ n14 + n12
Det
skal bemærkes at kø-afvist også indeholder det antal kunder der bliver
omstillet til den anden central (overløb) da disse også er udtryk for at
systemet er overbelastet.
Antal
nedkoblet i køerne forårsaget af abonnenten.
n15
= Abonnent pålægning i køerne.
Antal
nedkoblet i køerne forårsaget af abonnenten = n15
Samlede
antal nedkoblinger i køerne = n10
+ n14 + n12 + n15
Der
er i ”Antal ankommet til køerne”, inkluderet det antal abonnenter der bliver
afvist ( kø afvist ) før de får kømeldingen. Der skal derfor måles følgende for
at finde det antal abonnenter der ankommer til køerne.
n16
= Overløb og ingen ledig telefonist.
n17
= Ikke overløb og ingen ledig telefonist.
n18
= OFB og ingen ledig telefonist.
n19
= Time out og ingen ledig telefonist.
n20
= Gentag > 2 og ingen ledig telefonist.
Antal
ankommende til køerne = n17 +
n18 + n19 + n20
+ n21
Man
får så
|
Kønedkoblingsprocenten i alt = 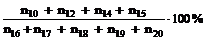
|
( 4-8 )
|
|
Kønedkoblingsprocenten forårsaget
af TDK = 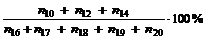
|
( 4-9 )
|
|
Kønedkoblingsprocenten forårsaget
af abonnenten = 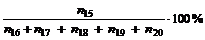
|
( 4-10 )
|
For
at få de mest nøjagtige tal vil det være den kontinuerte målemetode der skal
anvendes her, men man vil også kunne anvende skanne metoden. Som før nævnt skal
man for at kunne bruge skanne metoden, sørge for at intervallerne er så små, at
man ikke mister vigtige data pga. døgnrytmen.
Køtid.
Køtiden
er den tid fra en kunde ankommer i køen til denne får betjening eller bliver
afvist pga. time out. De tider hvor der sker en nedkobling, der ikke er
forårsaget af en time out, eller hvor kunden selv afbryder forbindelsen skal
ikke medtages, da disse værdier vil have en uønsket indvirkning på køtiden.
Dette skyldes at kunder der hurtigt afbryder forbindelsen eller forbindelsen
afbrydes pga. en defekt talemaskine, kunne forbedre køtiden og man ville derfor
kunne få det indtryk, at afviklingen af trafikken er i orden, hvor dette ikke
er tilfældet.
Denne
måling forudsætter at TDK kan udskille de tider, for kunder i kø, der selv har
afbrudt forbindelsen eller er blevet nedkoblet pga. en fejl i systemet. Det er
derfor ikke muligt at give et oplæg til hvordan denne måling skal fortages.
Det
er her nødvendigt både at kende middelværdien og variansen for at kunne danne
sig et overblik over hvordan køtiderne er fordelt. Grunden til det også er
nødvendigt at kende variansen er, at sandsynligheden for at få en tid der er
større eller mindre end middelværdien stiger, jo større variansen er i forhold
til middelværdien, se 4.4.1.
Middelværdien
og variansen bestemmes ved at dividere summen af de enkelte målinger med antal
målinger.
og
variansen findes ved følgende udtryk.
Kø-afvist.
Kø-afvist
er det antal kunder der afvises før de kommer i kø. Denne afvisning kan være
forårsaget af, at køen er fyldt eller længste ventetid er overskredet. Følgende
skal måles og summeres for at finde det antal kunder der bliver afvist
n21
= Kø-afvist der medfører overløb.
n22
= Kø-afvist der medfører nedkobling.
|
Kø afvist = n21 + n22
= n10
|
( 4-11 )
|
For
at få de mest nøjagtige tal, vil det være den kontinuerte målemetode der skal
anvendes her, men man vil også kunne anvende skanne metoden. Her gælder også at
man skal for at kunne bruge skanne metoden sørge for at intervallerne er så små
at man ikke mister vigtige data pga. døgnrytmen.
Total antal målinger.
Det
totale antal målinger der skal tages hvis de fastsatte værdier skal kunne
beregnes er
n1 = Manuel
CC, der udføres af telefonisten.
n2 = Auto
CC, der udføres af abonnenten.
n3 = Endt
service, hvor telefonisten selv oplyser det ønskede og derefter nedkobler
forbindelsen.
n4 = Abonnent
pålægning, hvor kunden selv fortage en pålægning efter endt oplæsning af
telefonnummer.
n5 = Abonnent
pålægning, hvor kunden har fortaget en pålægning før betjening.
n6 = Abonnent
pålægning, hvor kunden har fortaget en pålægning inden eller under første
kømelding.
n7
= OFB, Time out eller gentagelse af nummeret
er sket mere end to gange.
n8
= Antal
opkald til OP118.
n9 = Den
samlede tid det tager at betjene kunderne (Bemærk at n9 er en tid, og ikke et antal hændelser).
n10
= Kø afvist, der er det antal der afvises pga.
kø-fuld eller ventetiden er for lang.
n11
= Talemaskine ikke ledig, er det antal kunder
der afvises pga. for få eller defekte talemaskiner i køerne. Abonnent pålægning
i køerne.
n12
= Time out, der er det antal kunder der
afvises i køerne fordi ventetiden var for lang.
n14
= Talemaskine ikke ledig, der er de
nedkoblinger ASTDR talemaskinerne forårsager.
n15
= Abonnent pålægning i køerne.
n16
= Overløb og ingen ledig telefonist.
n17
= Ikke overløb og ingen ledig telefonist.
n18
= OFB og ingen ledig telefonist.
n19
= Time out og ingen ledig telefonist.
n20
= Gentag > 2 og ingen ledig telefonist.
Det
skal bemærkes at måling n11
= n14 + n15
For
få de mest nøjagtige tal anbefales som tidligere at anvende den kontinuerte
målemetode. Hvis en vis unøjagtighed kan accepteres, kan man anvende
skannemetoden. Man skal dog være opmærksom på, at ved anvendelse af
skannemetoden, skal alle målingerne fortages i de samme tidsintervaller, ellers
vil ideen med at sammenholde de forskellige værdier ikke være brugbar.
Ud fra de af TDK
udleverede materialer vil der her blive beskrevet hvilke målinger de foretager.
Opkald tilbudt.
Opkaldt tilbudt er
det antal opkald der tilbydes TDK, dvs. det samlede antal abonnenter der ringer
til OP118. Denne værdi indeholder også de kunder der kommer fra audiosvar.
Opkald besvaret.
Opkald besvaret er
det antallet af kunder der får en telefonist uanset om det drejer sig om
straksbesvarelse eller en kunde fra køerne. Denne værdi indeholder også de
kunder der afbryder forbindelsen under velkomstmeldingen.
Procent besvaret.
Procent besvaret er
defineret som ”opkald besvaret” i forhold til ”opkald tilbudt”
Middel ventetid.
Middelværdien af de
samlede tider over hvor længe de enkelte kunder befinder sig køen i forhold til
det samlede antal ankommende opkald til OP118. Denne værdi indeholder ikke
ventetid for ikke besvarede opkald.
Middelekspeditionstid.
Middelekspeditionstid
er den tid det tager en telefonist at besvare et opkald. Dvs. den tid der går
fra telefonisten modtager opkaldet til kunden viderestilles i systemet.
Opkald til kø.
Opkald til kø er
det antal kunder der ikke opnår straksbesvarelse. Denne værdi er inklusiv det
antal kunder der får kø-afvist.
Opkald afvist.
Opkald afvist er
det antal kunder der afvises med kø spæret (kø-afvist).
Antal pladser.
Antal pladser er en
middelværdi af antallet af ublokerede pladser. Dvs. en middelværdi af det antal
telefonister der har mulighed for at modtage et opkald.
Alfa.
Beskæftigelsesgraden
i procent der er en middelværdi, som angiver antallet af pladser med kunder i
forhold til ublokerede pladser.
Generelt for alle
målingerne gælder at disse fortages i Timeinterval og døgninterval.
Der vil i dette
kapitel blive fortaget en sammenligning af de forslåede målinger (se kap.4.3) med de målinger
TDK foretager (se kap.4.5).
Der vil derefter blive foretaget en endelig vurdering af de enkelte målinger,
som vil blive grundlaget for et endeligt forslag til TDK hvilke målinger der
vurderes relevante.
I skemaet (se Figur 4-4)
er der lavet en punktopstilling over hvilke målinger TDK laver og hvilke
målinger vi anbefaler.
|
TDK
|
Foreslået
|
|
Opkald tilbudt
|
Antal samlede
opkald
|
|
Opkald besvaret
|
Antal besvarede
opkald
|
|
Procent besvaret
|
Besvarelsesprocent
|
|
Middelventetid
|
Køtid
|
|
Middelekspeditionstid
|
Betjeningstid
|
|
Opkald til kø
|
Antal ankommende
til kø
|
|
Opkald afvist
|
Kø-afvist
|
|
Antal pladser
|
|
|
|
Nedkoblingsprocent
|
|
|
Kønedkoblingsprocent
|
|
Alfa værdi
|
|
Figur 4-4 Sammenligning af TDK og det foreslåede.
Fremhævet tekst: Målinger
som fortages eller ønskes fortaget og som indgår i statistikken.
Alm. tekst: Målinger
som fortages eller ønskes fortaget og som ikke indgår i statistikken.
Opkald tilbudt/Antal samlede opkald.
-
Opkaldt
tilbudt, er det samlede antal abonnenter der ringer til OP118 inklusiv de
kunder der kommer fra audiosvar.
-
Antal
samlede opkald, er det samlede antal kunder der ringer til OP118 ink de kunder
der har valgt OFB, har fået en Time out eller har fået gentaget nummeret mere
end to gange.
Ved
at sammenholde de to målinger, kan man se at de begge måler det samlede antal
kunder der ankommer til OP118. Derudover tager TDK de kunder med der kommer fra
audiosvar. Derved må forstås det antal kunder der har valgt OFB, har fået en
Time out eller har fået gentaget nummeret mere end to gange. Disse får enten
straksbetjening eller kommer fra køen.
Ved
at betragte Figur
4-3 ses man dermed ikke får de kunder med der bliver nedkoblet eller
afbryder forbindelsen i Recall queue’en og TDK vil derfor få en værdi der vil
kunne give en bedre ”Procent besvaret” end det reelt er tilfældet.
I
”Antal samlede opkald” er der valgt at måle OFB, Time out og Gentag>2
umiddelbart når disse hændelser indtræffer, og de kunder der derefter afbryder
forbindelsen, eller nedkobles inden de har får betjening, vil derfor blive
medregnet, og vil selvfølgelig få en negativ indflydelse på
Besvarelsesprocenten.
TDK
har på nuværende tidspunkt valgt at tage Opkald tilbudt med i deres statistik,
årsagen til dette er at få oplyst hvor mange kunder der ankommer til OP118. Da
dette vurderes at være relevant medtages Antal samlede opkald i statistik
skemaerne.
Opkald besvaret/Antal
besvarede opkald.
-
Opkald
besvaret, er antallet af kunder der får en telefonist. Denne værdi indeholder
også de kunder der afbryder forbindelsen under velkomstmeldingen.
-
Antal
besvarede opkald, er det antal kunder der forlader systemet efter end
betjening. Dette kan foregå ved pålægning, manuel- eller Auto CC, OFB, Time out
eller Gentag>2 (se kap.4.4).
Denne værdi indeholder også de kunder der afbryder forbindelsen under
velkomstmeldingen.
Da
de to værdier er ens vil de ikke vurderes nærmere, for nærmere uddybning se
kap.4.3.
Lige
som med Opkald tilbudt, har TDK på nuværende tidspunkt valgt at tage Opkald
besvaret med i deres statistik. Årsagen til dette kunne være en mulighed for at
se hvor mange der bliver serviceret i forhold til dem der har ringet til OP118.
Det vurderes ikke at være relevant, at medtage Opkald besvaret/Antal besvarede
opkald i statistikskemaerne, da Procent besvaret/Besvarelsesprocenten er rigelig
udtryk for hvor effektivt systemet er.
Procent
besvaret/Besvarelsesprocent.
-
Procent
besvaret, er ”opkald besvaret” i forhold til ”opkald tilbudt”.
-
Besvarelsesprocent,
er ”Antal besvarede opkald” i forhold til ”Antal samlede opkald”.
Da
der i de to forgående afsnit er valgt at bruge “Antal besvarede opkald” og
“Antal samlede opkald” eller ”opkald tilbudt”, er det naturligt at medtage
Besvarelsesprocenten i statistikskemaerne.
Middelventetid/Køtid.
-
Middelventetid
er middelværdien af de samlede tider over hvor længe de enkelte kunder har
befundet sig køen i forhold til det samlede antal ankommende opkald til OP118.
Denne værdi indeholder ikke ventetid for ikke besvarede opkald.
-
Køtid,
er middelværdien af de samlede tider over hvor længe de enkelte kunder har
befundet sig køen eksklusiv de kunder der selv nedkobler forbindelsen eller
bliver nedkoblet pga. tekniske problemer. Desuden skal variansen tillige
bestemmes ud fra disse målinger.
Der
er her tale om to måder at betragte køtiden på. Middelventetid er et udtryk for
hvor effektivt hele systemet er og dermed også et udtryk for serviceniveauet.
Værdien kan bruges til at se hvor længe en vilkårlig kunde i gennemsnit kan
forvente, at skulle vente inden denne bliver serviceret. Middelventetiden bruges
også af TDK i deres målsætning, se svartid bilag 1.
Køtid
er derimod et udtryk for, hvor længe en kunde, hvis denne sættes i kø, i
gennemsnit kan forvente at være i kø. Derudover bruges Køtid til at vurdere
hvor godt køerne afvikles. Da begge værdier synes relevante medtages de derfor
i statistikskemaet.
Middelekspeditionstid/Betjeningstid.
-
Middelekspeditionstid
er den tid det tager en telefonist at besvare et opkald. Dvs. den tid der går
fra telefonisten modtager opkaldet til kunden viderestilles i systemet.
-
Betjeningstid,
er den ”Samlede ekspeditionstid” i forhold til ”Antal samlede besvarede
opkald”.
De
disse to værdier er ens beskrives de ikke nærmere, for nærmere beskrivelse se
kap.4.3 og kap.4.5.
Opkald til kø/Antal
ankommende til kø.
-
Opkald
til kø, er det antal kunder der ikke opnår straksbesvarelse. Denne værdi er
inklusiv det antal kunder der får kø-afvist.
-
Antal
ankommende til kø, er det antal kunder der ikke opnår straksbesvarelse. Denne
værdi er inklusiv det antal kunder der får kø-afvist.
De
disse to værdier er ens beskrives de ikke nærmere, for nærmere beskrivelse se
kap.4.3 og kap.4.5
TDK
har på nuværende tidspunkt valgt at tage Opkald til kø med i deres statistik,
årsagen til dette kunne være en mulighed for at se hvor mange der bliver sat i
kø i forhold til dem der har ringet til OP118. Et andet udtryk for dette
forefindes hverken i TDK’s eller den foreslåede statistikopsamling og da denne
vurderes relevant medtages den i statistikskemaet.
Opkald afvist/Kø-afvist.
-
Opkald
afvist, er det antal kunder der afvises med kø spæret (kø-afvist).
-
Kø-afvist,
er det antal kunder der afvises med kø spæret (kø-afvist).
Da
disse to værdier er ens beskrives de ikke nærmere, for nærmere beskrivelse se
kap.4.3 og kap.4.5
Antal pladser.
-
Antal
pladser, er en middelværdi af antallet af ublokerede pladser. Dvs. en
middelværdi af det antal telefonister der har mulighed for at modtage et
opkald.
Man
vil ud fra antal pladser kunne få en ide om hvor belastet telefonisterne er, og
dermed også hvor effektivt de udnyttes. Det vurderes at denne værdi er relevant
og medtages derfor i statistikskemaet.
Alfa værdi.
-
Alfa
værdi, er en middelværdi, som angiver antallet pladser i forhold til antallet
af ublokerede pladser.
Da
denne værdi bruges i prioriteringen når der vælges telefonistgrupper, se kap.3.6, skal den medtages.
Der er i denne rapport ikke lavet et alternativ, da det er en værdi der har
stor betydning i systemet.
Nedkoblingsprocent.
-
Nedkoblingsprocent,
er ”Antal nedkoblet i kø” i forhold til ”Antal total nedkoblet”.
Da
TDK ikke har nogle sammenlignelig værdier for Nedkoblingsprocenten medtages
denne uden yderligere argumentation i den endelige statistikopsamling. For
yderligere uddybning af Nedkoblingsprocenten se kap.4.3.
Kønedkoblingsprocent.
-
Kønedkoblingsprocent,
er ”Antal nedkoblet i kø” i forhold til ” Antal ankommet til kø”.
Da TDK ikke har
nogle sammenlignelig værdier for Kønedkoblingsprocent medtages denne uden
yderligere argumentation i den endelige statistikopsamling. For yderligere
uddybning af Kønedkoblingsprocent se kap.4.3.
Ud fra det i kap. 4.6.1 vurderet skal
følgende målinger fortages.
|
TDK
|
Foreslået
|
Endelig
|
|
Opkald tilbudt
|
Antal samlede
opkald
|
Antal samlede opkald
|
|
Opkald besvaret
|
Antal besvarede
opkald
|
|
|
Procent besvaret
|
Besvarelsesprocent
|
Besvarelsesprocent
|
|
Middelventetid
|
Køtid
|
Middelventetid
|
|
|
|
Køtid
|
|
Middelekspeditionstid
|
Betjeningstid
|
Betjeningstid
|
|
Opkald til kø
|
Antal ankommende
til kø
|
Antal ankommende til kø
|
|
Opkald afvist
|
Kø-afvist
|
Kø-afvist
|
|
Antal pladser
|
|
Antal pladser
|
|
|
Nedkoblingsprocent
|
Nedkoblingsprocent
|
|
|
Kønedkoblingsprocent
|
Kønedkoblingsprocent
|
|
Alfa
|
|
Alfa
|
Figur 4-5 De endelige målinger.
Fremhævet tekst: Målinger
som fortages eller ønskes fortaget og som indgår i statistikken.
Alm. tekst: Målinger
som fortages eller ønskes fortaget og som ikke indgår i statistikken
Generelt.
TDK har valgt at
fortage målingerne i time- og døgnintervaller, hvilket stemmer overens med de i
kap.4.3 ønskede
intervaller. Dog er der i kap.4.3
også nævnt at foretage målingerne i uge-, måned-, og årintervaller. Dette kunne
være relevant, for at kunne få et mere nuanceret overblik over
trafikfordelingen. Derudover kunne det være relevant at se målingerne i
årsintervaller, for at se om servicens popularitet er stiende eller faldende.
Udover at
målingerne skal fortages for den enkelte telefonist og telefonistgruppe og
endelig for hele systemet ville en opdeling af
Danmark i øst og vest også være hensigtsmæssig, da det er de områder de to
centraler hver især dækker. Dette er også tilfældet for TDK’s statistik
opsamling.
Et forslag til
hvordan en tabel til samling af den endelige statistik kunne have for som vist
i Figur 4-6.
Der er her både taget højde for døgn- og timeintervaller. Tabelformen vil være
brugbar til den enkelte telefonist, telefonistgruppe og region ( kddsa og khdsa
).
|
Interval
|
Antal samlede opkald
|
Besvarelses procent
|
Middel ventetid
|
Køtid
|
Betjenings tid
|
Antal ankomende til kø
|
Kø afvist
|
Nedkoblings procent
|
kønedkoblings procent
|
Antal pladser
|
Alfa værdi
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sum
|
sum
|
sum
|
sum
|
sum
|
sum
|
sum
|
sum
|
sum
|
sum
|
sum
|
sum
|
Figur 4-6 Eksempel på
Data oversigt.
Det skal bemærkes
at intervallerne kan være timer, døgn, uger eller måneder. Den nederste række
er en sum af kolonnerne, således at man med timeintervaller får summen for hele
døgnet osv.
De to mest
interessante størrelser er Besvarelsesprocent (Fremkommelighed) og
Middelventetid (svartid) som TDK har opstillet målsætninger for, se bilag 1.
Der er i dette
kapitel forsøgt at vurdere og optimere TDK’s statistik. Vurderingen af hvilken
statistik vi har ment er relevant er fortaget ud fra det i kap.3.9 konstrueret
tilstandsdiagram. Da vi ikke har haft kontakt med de personer der arbejder med
statistikken og fået deres vurdering, kan der stadig, efter deres opfattelse,
være mangler. Det endelige forslag, i dette kapitel, er derfor kun et forslag
til hvordan det kunne gøres. Det er herefter op til TDK at vurdere om de
forslåede ændringen er så relevante, at det kan betale sig at ændre den
nuværende statistikopsamling.
Vores vurdering er
dog, at der vil være adskillige fordele ved at anvende den forslåede
statistikopsamling frem for den nuværende, også selv om de ligner hinanden
meget. Dette kan begrundes med at den forslåede statistik giver et mere
detaljeret indblik i hvad der sker i systemet, herunder lokalisering af svage
områder i systemet, eller et overblik over hvor mange kunder der enten bliver
nedkoblet eller selv afbryder forbindelsen og hvor denne nedkobling foregår.
En af de vigtigste
målinger i statistikken er Besvarelsesprocenten (fremkommeligheden), da denne
værdi indgår i TDK’s målsætninger, se bilag 1.
Hvis man kigger på
Besvarelsesprocenten er den, som i kap.4.3
beskrevet, et udtryk for hvor effektivt den ankommende trafik afvikles. Dvs. jo
færre der bliver serviceret af det antal kunder der ringer til oplysningen, jo
lavere bliver Besvarelsesprocenten. TDK’s målsætning er at 95% af de kunder der
ringer ind til oplysningen i hverdagene skal serviceres, hvilket betyder at kun
5% må blive nedkoblet. Nedkoblingen kan enten
være forårsaget af TDK eller af kunden som beskrevet i kap.4.3.
Det er ikke muligt,
ud fra TDK’s statistik, at vurdere hvilken af disse to typer nedkoblinger der
er mest betydende, for en dårlig Besvarelsesprocent. Med den endelige
statistikopsamling, har man derimod mulighed for at lokalisere problemet, med
en lav Besvarelsesprocent, ved at betragte Køtid, Kø-afvist, Nedkoblingsprocent
og Kønedkoblingsprocent. Det er netop en af de ting der gør at den endelige
statistik opsamling er væsentligt forbedret i forhold til TDK’s.
En anden vigtig
værdi er Betjeningstiden (Middelekspeditionstid), som er et udtryk for hvor
hurtigt kunderne bliver serviceret af telefonisten (se kap.4.3). Hvis
betjeningstiden vurderes for høj, er der hverken i den nuværende eller endelige
statistik, nogen mulighed for bestemme årsagen hertil.
Da telefonisterne
betjener andre tjenester end oplysningen og disse er behæftet med en
prioritering (se kap.3.6)
vil en omprioritering måske hjælpe. En omprioritering kunne bevirke, at
telefonisterne kunne få en større rutine i betjening af enkelte tjenester, som
ville medvirke til en lavere betjeningstid. Man kunne foreksempel forstille sig
at OPS først søgte efter de telefonister der har det enkelte kald som
førsteprioritet, og ikke som nu, de telefonister der har mindst at lave.
Udover at
kontrollerer TDK’s målsætning, giver den forslåede statistik også et meget mere
overskueligt og detaljeret indblik i hvordan trafikken er fordelt i løbet af
timer, dage, uger, måneder og år. Det vil derfor hurtigt være muligt, at
bestemme evt. tendenser i trafikken, som kunne bruges til dimensionering af nye
systemer og optimering af det gamle. Hvis det af TDK vurderes at det ville være
relevant at ændre deres oversigt over statistikken, ville dette være
forholdsvis nemt.
Det har ikke være
muligt at vurdere hvordan målingerne skal fortages, og om de overhovedet kan
fortages, hvilket gør projektet meget fiktivt. Det må derfor være op til TDK at
foretage disse vurderinger. Efter vores overbevisning er der dog stadig stof nok
til et nyt projekt, som skulle koncentrere sig mere om selve målemetoderne samt
den praktiske realisering af dataopsamlingen.
Til optimering og
dimensionering af brugen af eksterne ressourcer anvendes teletrafik teorien.
Teletrafik teorien er en gren af matematikken, der anvender
sandsynlighedsregning, til løsning af problemer i forbindelse med planlægning,
drift og vedligeholdelse af telesystemer. Vha. teletrafik teorien kan
matematiske modeller opstilles og anvendes til at måle veldefinerede størrelser
i teletrafikken. Hermed dannes et grundlag for vurderinger af teletrafik
systemets kapacitet og fremtidige trafikbehov.
Med teletrafik
teorien som værktøj, kan et eksisterende system analyseres og optimeres,
hvilket følgelig kan resultere i ressource besparelser. På den anden side, kan
det vise sig at et eksisterende system skal udvides, for at klare den ønskede
belastning.
For at kunne
optimere og dimensionere ressourcerne i OP118 tjenesten, ved hjælp af teletrafikteori,
er det nødvendigt at opstille en matematisk model over systemet.
Der lægges først ud
med en introduktion til teletrafikteori, og derefter vil der blive udarbejdet
en forholdsvis simpel model og de karakteristiske størrelser for denne model
bestemmes. Herefter vil modellen blive udvidet gradvis med henblik på at tilnærme
den bedst muligt til OP118 systemet.
Der vil i dette
kapitel blive givet en kort gennemgang af de forskellige begreber og størrelser
inden for teletrafikteori. Gennemgangen vil dog kun omfatte de begreber og
størrelser som er nødvendig at kende, for at kunne forstå de udregninger og
betragtninger der bliver gjort i kap.6.
Hvis man allerede
har et godt kendskab til teletrafikteori og ikke ønsker en opfriskning vil det
ikke være nødvendigt at læse dette kapitel. Kapitlet er skrevet på basis af
[1], men visse emner er dog uddybet pga. forståelsen og for at kunne anvende
teorien til udvikling af matematiske modeller for OP118.
Inden for
teletrafikteorien anvendes flere forskellige kø typer. For alle kø typer
gælder, at de består af et system med n
ensartede betjeningssystemer med fuld fremkommelighed.
At et system har
fuld fremkommelighed betyder, at et kald kun afvises hvis alle ledninger er
optaget og at alle ledninger er identiske. Dette betyder, at hvis blot én
ledning er ledig, kan et opkald få fat i den. Hvis alle betjeningssteder er
optaget, men der stadig er ledige ledninger, bliver opkaldet placeret i en kø
hvor det venter på at et betjeningssted bliver ledig.
I et køsystem kan
man anvende forskellige kødiscipliner. Kødisciplinen er bestemmende for i
hvilken rækkefølge kunder udtages fra køen til betjening, og der findes tre
klassiske kødiscipliner
FIFO First In First Out. Denne kødisciplin
kaldes ofte en retfærdig kø eller en ordnet kø og er den mest anvendte
kødisciplin, når det drejer sig om betjening af mennesker i kø. Betegnelsen
FCFS First Come First Served ses tillige anvendt.
Med FIFO menes at den der først er kommet i kø også kommer først ud af køen og
ikke nødvendigvis først ud af hele systemet, da betjeningstiden er
eksponentialfordelt.
LIFO Last
In First Out. Denne kødisciplin anvendes f.eks. i computere ved håndtering af
en stack, eller f.eks. på butikshylder hvor dåsen der sidst blev sat på plads
først bliver taget ned igen. LIFO betegnes også LCFS Last Come First Served.
SIRO Service
In Random Order. Denne kødisciplin betyder at alle kunder i køen har lige stor
sandsynlighed for at blive udtaget af køen til betjening. Betegnelserne RANDOM
og RS (Random Selection) anvendes også.
I litteraturen
findes der en meget udbredt notation der beskriver hvordan en trafik afvikles i
et givet system. Følgende notation er indført for kømodeller.
A
/ B / n
hvor
A = ankomstproces.
B = betjeningsfordeling.
n = antal
betjeningssteder.
For A og B anvendes
følgende standardiserede forkortelser.
W = Markovian.
Eksponentialfordelte tider og poisson fordelte ankomstproces.
D = Determistisk.
Konstante tider.
Ek = Erlang
– k – fordelte tider (E1 = M).
Hn =
Hypereksponentielfordeling af n’te
orden.
G = General.
Vilkårlig tidsfordeling.
GI = General
Independent, renewal ankomstproces.
PH = Phase – type, Fase – type
fordeling.
Cox = Cox-fordeling.
For en fuldstændig
specifikation af køsystemet anvendes der yderligere 3 symboler. Der er ikke
almindelig enighed om rækkefølgen eller betydningen af disse symboler, men det
vil altid fremgå hvilken rækkefølge og betydning der anvendes. I denne rapport
anvendes følgende notation.
A / B / n / K / S / X
hvor
K = systemets
totale kapacitet.
S = kundepopulationens
størrelse.
X = anvendt
kødisciplin.
Hvis intet andet
fremgår, vil K = S = ¥, og hvis intet andet er nævnt vil der tillige være
tale om et system med fuld fremkommelighed.
Som nævnt overfor,
anvendes statistik og sandsynlighedsregning i teletrafik teorien, derfor
gennemgås her kort nogle definitioner inden for sandsynlighedsregning på basis
af [4].
Eksperimenter, udfald og hændelser.
I
sandsynlighedsregning er det nødvendigt at fremskaffe data til bearbejdning.
Dette kan gøres enten ved kontrollerede forsøg eller observationer. Dette
kaldes eksperimenter. Eksperimentet resulterer i et udfald eller prøve punkt
(prøve som i stikprøve), og mængden af alle mulige udfald kaldes prøve mængden
S, og delmængder af S kaldes hændelser. Det er især eksperimenter med
tilfældige udfald der er interessant.
Sandsynlighed.
Sandsynligheden for
en hændelse i et eksperiment er et mål for hvor ofte denne hændelse forekommer
ved mange forsøg. Sandsynligheden P(A) for en hændelse A er da
|

|
( 5-1)
|
De mulige udfald
skal tilhøre en fællesmængde A af eksperimentets mulige udfald, mængden S
|

|
|
Figur 5-1,
Eksperimentmængden S, indeholdende udfaldsmængden A.
|
Stokastiske variable, fordelingsfunktion og
tæthedsfunktionen.
Inden for
teletrafik teori viser det sig at tidsintervaller så som betjeningstider,
perioder med spærring, ventetider, svartider, afstande mellem
opkaldstidspunkter osv. er af tilfældige varigheder, derfor vil et tidsinterval
X være en stokastisk variabel. Og da alle tidsintervaller er positive, regnes
kun med ikke negative stokastiske variable. Fordelingsfunktionen defineres
således: 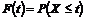 hvor X er en
stokastisk variabel. Fordelingsfunktionen beskriver for alle t sandsynligheden
for at X kan antage enhver værdi der ikke er større end t. Normalt forudsættes
det at fordelingsfunktionen er differentiabel
hvor X er en
stokastisk variabel. Fordelingsfunktionen beskriver for alle t sandsynligheden
for at X kan antage enhver værdi der ikke er større end t. Normalt forudsættes
det at fordelingsfunktionen er differentiabel
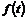 kaldes enten
tæthedsfunktionen, frekvensfunktion eller sandsynlighedsfunktionen, og angiver
sandsynligheden for at
kaldes enten
tæthedsfunktionen, frekvensfunktion eller sandsynlighedsfunktionen, og angiver
sandsynligheden for at 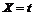 .
.
Poissonprocessen.
I teletrafikteorien
beskrives ankomstprocesser ofte bedst med poissonprocessen, som er den mest
tilfældige proces der findes. Jo mere indviklet, tilfældigt og uoverskueligt en
proces er, desto bedre beskrives processen af poissonprocessen.
Karakteristiske
egenskaber for poissonprocessen er stationaritet, uafhængighed i alle
tidspunkter og regularitet.
Stationaritet eller statistisk ligevægt.
Stationaritet
betyder at de sandsynlighedsfordelinger der er tilknyttet processen er
uafhængige af det absolutte tidspunkt. Stationaritet defineres således
|
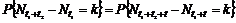
|
( 5-2)
|
Dvs. at
sandsynligheden for at få et vilkårligt antal hændelser k i et vilkårligt tidsinterval [t1,
t1 + t2[ er uafhængig af tidspunktet t1. Begrebet statistisk ligevægt anvendes tillige om
stationaritet.
Uafhængighed.
Uafhængighed
betyder at de hændelser der forekommer er uafhængige af hvilke hændelser der
tidligere er indtruffet, dvs. at processens videre forløb kun er afhængig af
den øjeblikkelige tilstand. Uafhængighed defineres således
|
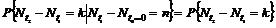
|
( 5-3)
|
Dvs. at
sandsynligheden for at der indtræffer k
hændelser i tidsintervallet [t1, t1 + t2[ er uafhængig af hvor mange hændelser der er
indtruffet før t1. Hvis
dette gælder for alle t, kaldes
processen en Markovproces, dvs. at hændelser der sker efter et givet tidspunkt
kun er afhængig af den øjeblikkelige tilstand og ikke af tidligere hændelser.
Regularitet.
En proces er
regulær, hvis sandsynligheden for at der indtræffer mere end én hændelse til et
tidspunkt er nul.
|
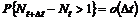
|
( 5-4)
|
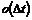 er en såkaldt
nulfunktion, dvs. at
er en såkaldt
nulfunktion, dvs. at 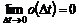 .
.
F.eks. vil
tidspunkter for malkning af køer, i en stald, med kun én malkemaskine, følge en
regulær proces, da kun én ko kan begynde med at blive malket af gangen, mens
antallet af kopatter der bliver malket, vil følge en irregulær proces, da op
til fire kopatter kan begynde med at blive malket samtidigt.
Trafik.
Med trafik eller
trafikintensitet menes der trafik pr. tidsenhed. Enheden for trafikintensitet
er erlang, og er opkaldt efter den
danske matematiker A. K. Erlang. Enheden skrives som [e] eller [erl.] og er
dimensionsløs. Det er vigtigt at skelne mellem de to begreber trafikintensitet
og opkaldsintensitet.
-
Trafikintensitet
er som nævnt overfor trafik pr. tidsenhed, og regnes i enheden erlang som er
dimensionsløs.
-
Opkaldsintensitet
er det gennemsnitlige antal opkald der tilbydes pr. tidsenhed og regnes i
erlang pr. tidsenhed.
Tilbudt trafik.
Den tilbudte trafik
er den mængde trafik der kan afvikles i et system når ingen opkald bliver
afvist, dvs. den mængde trafik der vil blive afviklet, hvis der er et
ubegrænset antal betjeningssteder. Denne størrelse er en fiktiv størrelse, der
som regel bestemmes ud fra den afviklede trafik. Den tilbudte trafik kan
estimeres ud fra opkaldsintensiteten l og
middelbelægningstiden s, ud fra den
betragtning at den tilbudte trafik er det gennemsnitlige antal opkald pr.
middelbelægningstid
Som det ses, er
enheden for den tilbudte trafik A
erlang (dimensionsløs).

Eksempel.
Hvis f.eks. et
system med en opkaldsintensitet på 5 opkald pr. minut, og middelbelægningstiden
er 3 minutter, så er den tilbudte trafik 15 erlang
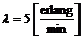
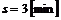
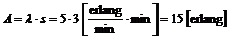
Eksemplet kan også
vises med følgende figur
I Figur 5-2 bliver der tilbudt 5 opkald pr. minut, og alle kald
afvikles på 3 minutter. Som det ses, vil der efter et kort tidsforløb være 15
kunder i systemet til enhver tid. Dvs. at der tilbydes systemet en trafik på 15
opkald på 3 minutter.
Afviklet trafik.
Den mængde trafik
der rent faktisk bliver afviklet i et system kaldes den afviklede trafik, AC = A’. Hvis man taler om den afviklede trafik i et givet tidsinterval,
menes der det gennemsnitlige antal opkald der er blevet afviklet i dette
tidsinterval, dvs. middelværdien af trafikintensiteten i dette tidsinterval.
Hvis 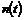 er det antal af
betjeningssteder der er optaget til tiden t,
kan følgende udtryk opstilles
er det antal af
betjeningssteder der er optaget til tiden t,
kan følgende udtryk opstilles
En betingelse for ( 5-5) er at ingen trafik bliver afvist
pga. at systemet har for lille kapacitet, hvis opkald bliver afvist, så
refereres der til disse afviste opkald med Al
= A’’.
I teletrafik
teorien er eksponentialfordelingen den absolut vigtigste tidsfordeling, da den
har vist sig at give en forbavsende god beskrivelse af mange fysiske
tidsintervaller. Denne fordeling kaldes også ”den negative
eksponentialfordeling”. Fordelingen er karakteriseret ved en enkelt parameter,
intensiteten l, der et mål for hvor mange hændelser der indtræffer
pr. tidsenhed.
Fordelingsfunktionen.
|
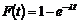
|
( 5-6)
|
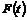 angiver som nævnt
tidligere sandsynligheden for at et tidsinterval ligger i intervallet [0 .. t]. Ved at skitsere
angiver som nævnt
tidligere sandsynligheden for at et tidsinterval ligger i intervallet [0 .. t]. Ved at skitsere 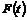 , ses det hvilken indflydelse opkaldsintensiteten l har på
fordelingsfunktionen. Karakteristiske størrelser som asymptoter og begyndelses
tangent bestemmes først.
, ses det hvilken indflydelse opkaldsintensiteten l har på
fordelingsfunktionen. Karakteristiske størrelser som asymptoter og begyndelses
tangent bestemmes først.
Asymptote for 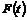 når
når 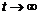
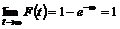
Tangent for 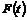 når
når 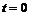
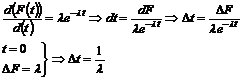
Som det ses i Figur 5-3
vil kurven for fordelingsfunktionen blive stejler ved større intensitet, l. Dvs. at ved
en stigende opkaldsintensitet vil tidsintervallet med stigende sandsynlighed
blive mindre.
Frekvensfunktionen.
|
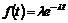
|
( 5-7)
|
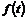 angiver som nævnt
tidligere sandsynligheden for at et tidsinterval antager værdien t. Ved at skitsere
angiver som nævnt
tidligere sandsynligheden for at et tidsinterval antager værdien t. Ved at skitsere 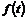 , ses det hvilken indflydelse intensiteten l har på
frekvensfunktionen. Karakteristiske størrelser som asymptoter og begyndelses
tangent bestemmes først.
, ses det hvilken indflydelse intensiteten l har på
frekvensfunktionen. Karakteristiske størrelser som asymptoter og begyndelses
tangent bestemmes først.
Asymptote for 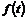 når
når 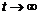
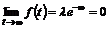
Tangent for 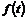 når
når 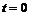
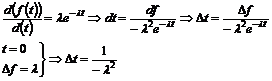
Af Figur 5-4
fremgår det at ved stigende intensitet, vil sandsynligheden for at et
tidsinterval antager en bestemt størrelse blive mindre.
Generelt kan det
siges at jo større intensitet l, jo mindre bliver tidsintervallerne.
Da det er ofte er
utilstrækkelig med en eksponentialfordeling for at beskrive et system, er der
udviklet metoder der beskriver et system med flere eksponentialfordelinger.
Conny Palm har indført to fordelings klasser, stejle- og flade fordelinger, se
kapitel 4 i [1]. Man får en stejl fordeling ved at forbinde et antal
eksponentialfordelinger i serie, og en flad fordeling ved at forbinde i
parallel. Det kan vises, at hvis man kombinerer stejle- og flade fordelinger
kan man tilnærme en hvilken som helst fordeling med en vilkårlig tilnærmelse.
[1] viser i kap.
7.1.1 hvordan man bestemmer tilstandssandsynligheden 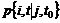 som er sandsynligheden
for at finde i opkald i systemet til
tiden t, under den forudsætning at
der til tiden t0 var j opkald i systemet. Denne
tilstandssandsynlighed refereres ofte med
som er sandsynligheden
for at finde i opkald i systemet til
tiden t, under den forudsætning at
der til tiden t0 var j opkald i systemet. Denne
tilstandssandsynlighed refereres ofte med 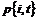 .
.
Hvis man betragter
et lille tidsinterval 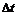 , får man, idet l er
opkaldsintensiteten, antal kunder der ankommer pr. tidsenhed, og m er dødintensiteten, antal kunder der bliver
afviklet pr. tidsenhed
, får man, idet l er
opkaldsintensiteten, antal kunder der ankommer pr. tidsenhed, og m er dødintensiteten, antal kunder der bliver
afviklet pr. tidsenhed
1. Sandsynligheden for at et opkald starter i
intervallet 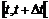 er ligefrem
proportional med
er ligefrem
proportional med 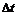 og uafhængig af det
absolutte tidspunkt t. Dvs. at
sandsynligheden for at ét opkald begynder i dette tidsinterval er
og uafhængig af det
absolutte tidspunkt t. Dvs. at
sandsynligheden for at ét opkald begynder i dette tidsinterval er
Se iøvrigt afsnittet om stationaritet i kap. 5.2.3.
2. Ganske tilsvarende er sandsynligheden for at
et eksisterende opkald afsluttes i 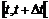 ligefrem proportional
med
ligefrem proportional
med 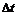 og uafhængig af det
absolutte tidspunkt t. Derfor er
sandsynligheden for at ét opkald afsluttes i dette interval
og uafhængig af det
absolutte tidspunkt t. Derfor er
sandsynligheden for at ét opkald afsluttes i dette interval
Hvis der findes i opkald i systemet i
forvejen til tiden t, så er
sandsynligheden for at ét af disse opkald afsluttes i gange større
Dvs. at jo flere kunder der er i systemet, jo størrer er sandsynligheden for at
en af kunderne vil forlade systemet i 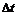 .
.
3. Da der forlanges regularitet, må der ikke
forekomme tvillingefødsler, dvs. at sandsynligheden for at to hændelser
indtræffer samtidigt samtidig skal gå mod nul. F.eks. vil sandsynligheden for
at to opkald i 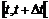 være
være
Sandsynligheden for at der både ankommer og afsluttes et opkald i 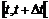 er da
er da
|
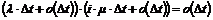
|
( 5-8)
|
Ved at undersøge
alle muligheder for at der eksisterer i
opkald til tiden 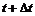 og lade
og lade 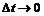 kan man ved hjælp af
et uendeligt antal differentialligninger bestemme tilstandssandsynligheden
kan man ved hjælp af
et uendeligt antal differentialligninger bestemme tilstandssandsynligheden 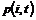 .
.
Først undersøges
mulighederne for at have nul opkald til 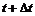 . Det kan ske på følgende måder
. Det kan ske på følgende måder
1. Ingen
opkald eksisterer før t, og ingen
opkald starter i 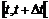 .
.
2. Ét
opkald eksisterer til t og ophører i 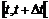
|
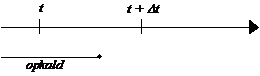
|
|
Figur
5-5, Ét eksisterende opkald afsluttes i
[t, t + Dt [ og resulterer i nul eksisterende opkald.
|
3. To
eller flere opkald eksisterer til t
og ophører alle i 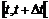 .
.
Ad. 1
Sandsynligheden for
at der ikke startes et opkald i 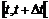 er
er
Ad. 2
Sandsynligheden for
at kun ét eksisterende opkald ophører i 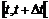 er
er
Ad. 3
Som vist tidligere,
er sandsynligheden for to eller flere hændelser i 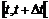 lig
lig 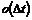 .
.
Derfor kan det
siges at sandsynligheden for at der er nul opkald i systemet til tiden 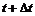 er
er
|
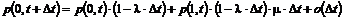
|
( 5-9)
|
Hernæst undersøges
mulighederne for at der eksisterer flere end nul opkald til  . I de følgende figurer er det som et eksempel illustreret
hvorledes det er muligt at have i = 2
opkald til tiden
. I de følgende figurer er det som et eksempel illustreret
hvorledes det er muligt at have i = 2
opkald til tiden  . Dvs. at
. Dvs. at 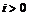 .
.
|
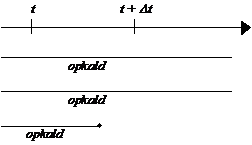
|
|
Figur
5-6, Et opkald ophører i [t, t
+ Dt[, 2 opkald eksisterer til t + Dt.
|
Sandsynligheden for
at få ét opkald mindre til 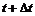 end der var til tiden t
end der var til tiden t
Hvor 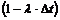 er sandsynligheden for
at ingen opkald påbegyndes i
er sandsynligheden for
at ingen opkald påbegyndes i 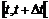 og
og 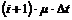 er sandsynligheden for
at et opkald ophører i
er sandsynligheden for
at et opkald ophører i 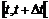 når der eksisterer i + 1 opkald til tiden t.
når der eksisterer i + 1 opkald til tiden t.
|
|
|
Figur
5-7, Ingen hændelser i [t, t
+ Dt[, 2 opkald eksisterer til t og t + Dt.
|
Sandsynligheden for
at der ingen hændelser sker i 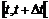 er
er
Hvor 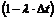 er sandsynligheden for
at ingen opkald påbegyndes i
er sandsynligheden for
at ingen opkald påbegyndes i 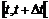 og
og 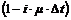 er sandsynligheden for
at ingen ophører i
er sandsynligheden for
at ingen ophører i 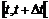 når der eksisterer i opkald til tiden t.
når der eksisterer i opkald til tiden t.
|
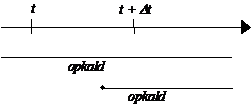
|
|
Figur
5-8, Et opkald ankommer i [t, t
+ Dt[, 2 opkald eksisterer til t + Dt.
|
Sandsynligheden for
at få ét opkald mere til 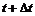 end der var til tiden t
end der var til tiden t
Hvor 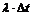 er sandsynligheden for
at et opkald påbegyndes i
er sandsynligheden for
at et opkald påbegyndes i 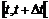 og
og 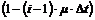 er sandsynligheden for
at et opkald ikke ophører i
er sandsynligheden for
at et opkald ikke ophører i 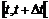 når der eksisterer i - 1 opkald til tiden t.
når der eksisterer i - 1 opkald til tiden t.
Sammenlagt kan
følgende udtryk opstilles
og ( 5-10) kan omskrives således
|
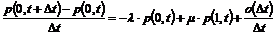
|
[1]-7.5
|
Dette er en
differentialligning, og lader man 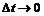 findes
findes
|
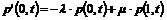
|
[1]-7.7
|
[1]-7.7 skal
opfattes således at intensitetsændringen til tiden t i tilstand 0 er lig med den intensitet som systemet skifter fra
tilstand 1 til tilstand 0 minus den intensitet som systemet skifter fra
tilstand 0 til tilstand 1. Ved at omskrive [1]-7.4 fås et tilsvarende udtryk
for en vilkår tilstand i
|
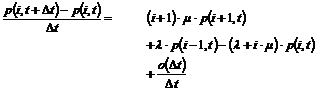 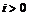
|
[1]-7.6
|
[1]-7.6 er også en
differentialligning, og lader man igen 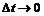 findes
findes
|
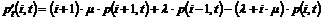 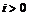
|
[1]-7.8
|
Som er
sandsynligheden for at komme til tilstand i
til tiden t. [1]-7.8 siger at den
samlede intensitetsændring i en vilkårlig tilstand i er den samlede intensitet der strømmer til tilstand i fra andre tilstande minus den
intensitet der strømmer væk fra tilstand i.
Da systemet er lukket, vil summen af intensitetsændringer være nul
|
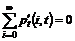
|
( 5-11)
[1]-7.9
|
Ved at betinge at
der er statistisk ligevægt, dvs. at ingen parametre er tidsafhængige, kan
følgende tre udtryk opstilles (se [1]-s135)
|
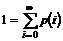
|
( 5-12)
|
Disse
differentialligninger kan løses og udtrykkes ved 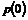 og det er gjort i
[1]-s.135-136
og det er gjort i
[1]-s.135-136
|
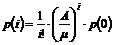
|
[1]-7.19
|
|
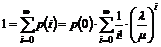
|
[1]-7.20
|
|
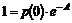
|
[1]-7.21
|
|
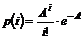
|
( 5-13)
[1]-7.22
|
Hvor p(i)
er sandsynligheden for at komme i en vilkårlig tilstand, og A er den tilbudte
trafik, dvs. det gennemsnitlige antal opkald pr. middelbelægningstid
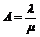 .
.
I [1] er der blevet
udviklet en model for et afvisningssystem med uendeligt mange ledninger
(således der ikke optræder spærring), poisson ankomstproces og eksponentielle
belægningstider. Denne model er baseret på at kunne bestemme med hvilke
sandsynligheder et system skifter fra at en ledning mere eller mindre optaget.
I Figur 5-9 er alle systemets tilstande, dvs. antallet af optagne
ledninger, vist som cirkler, og intensiteterne hvormed systemet skifter mellem
tilstandene er vist med pile. Pga. regularitet, sker der kun én hændelse af
gangen, og der kan kun skiftes til en af nabotilstandene.
Da systemet
betragtes i et tidsinterval hvor ingen af parametrene ændrer sig, stationaritet
eller statistisk ligevægt, vil antallet af tilstandsskift til en vilkårlig
tilstand i være lig antallet af skift
fra denne tilstand. Ligevægtssandsynligheden 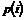 defineres til at være
sandsynligheden for at komme i tilstand i
og vil dermed også være den brøkdel at tiden som systemet er i tilstand i. Dermed kan følgende generelle
betragtninger foretages.
defineres til at være
sandsynligheden for at komme i tilstand i
og vil dermed også være den brøkdel at tiden som systemet er i tilstand i. Dermed kan følgende generelle
betragtninger foretages.
Tilstandsskiftintensiteter.
Den intensitet som
antal optagne ledninger skifter med kan forklares således
- Voksende antal optagne ledninger.
Da der er uendelig mange kunder, så vil opkaldsintensiteten være uafhængig af
hvor mange kunder der er i systemet. Dvs. at antal optagne ledninger vokser med
konstant intensitet, nemlig opkaldsintensiteten l, der er
antal opkald pr. tidsenhed.
- Faldende antal optagne ledninger.
Når der er netop én kunde i systemet, én optaget ledning, og
middelbelægningstiden eller middelbetjeningstiden er
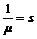
så vil systemet skifte fra én til nul optagne ledninger med intensiteten m, der er antal betjente kunder pr.
tidsenhed. Hvis der er to optagne ledninger, så vil systemet skifte fra to til
én optagne ledninger med den dobbelte intensitet, 2m, osv.
Dvs.
at
-
Systemet
skifter i gennemsnit l gange fra
tilstand i – 1 til tilstand i pr. tidsenhed systemet er i tilstand i - 1.
-
Systemet
skifter i gennemsnit (i + 1)m gange fra tilstand i + 1 til tilstand i pr.
tidsenhed systemet er i tilstand i +
1.
-
Systemet
skifter i gennemsnit (im + l) gange fra
tilstand i til tilstand i + 1 eller i - 1 pr. tidsenhed systemet er i tilstand i.
Af
disse betragtninger fås følgende
|
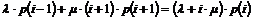
|
[1]-7.23
|
Intensiteternes
størrelse kan indføres i Figur 5-9.
Denne
metode gælder selvfølgelig kun når der er statistisk ligevægt, og er en meget
simpel metode til at opstille ligevægtsligninger for vilkårlige
springintensitetsdiagrammer.
Ved
at ligge et snit mellem tilstand i –
1 og i, ses det at hvis systemet er i
statistisk ligevægt, vil det skifte lige mange gange fra tilstand i – 1 til i som fra i til i – 1. Denne anskuelse kan gøres for
alle tilstande og generelt kan man skrive
|

|
( 5-14)
[1]-7.24
|
Desuden
antages det at alle tilstande for systemet er opnåelige, hvilket betyder at
|
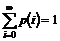
|
( 5-15)
[1]-s137
|
Systemer med et
begrænset antal ledninger
Systemet
der er vist i Figur 5-9 har en uendelig kapacitet, og er
derfor uinteressant i dette projekt. Derfor opstilles et lignende system med et
endeligt antal ledninger n, poisson
ankomstproces og eksponentialfordelt ankomstproces.
|
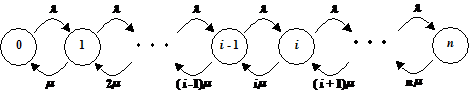
|
|
Figur 5-10, Trunkeret Poissonfordeling.
|
Sådan
et system kaldes en trunkeret poissonfordeling eller ”Erlang-fordeling”.
Ligevægtssandsynlighederne for dette system bestemmes efter samme princip som
vist ovenfor, og der kan findes en entydig løsning til alle
tilstandssandsynligheder
Af ( 5-16) kan 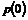 nu bestemmes
nu bestemmes
|
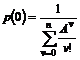
|
( 5-17)
|
Hvor
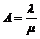 er den tilbudte
trafik.
er den tilbudte
trafik.
I
det følgende bestemmes de karakteristiske størrelser for systemet bestemmes.
Tidsspærring.
En
særlig interessant størrelse er 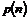 som angiver
sandsynligheden for at alle ledninger i systemet er optaget, dvs. at der i
denne situation både vil være opkaldsspærring og tidsspærring. Tidsspærring er
altså den brøkdel af tiden hvor alle fremkommelige ledninger er optaget.
som angiver
sandsynligheden for at alle ledninger i systemet er optaget, dvs. at der i
denne situation både vil være opkaldsspærring og tidsspærring. Tidsspærring er
altså den brøkdel af tiden hvor alle fremkommelige ledninger er optaget.
Dette
udtryk er kendt som Erlangs B-formel, eller Erlangs første formel, og er meget
berømt. Den betegnes ofte med 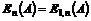 og er som det ses kun
en funktion af den tilbudte trafik og antallet af ledninger.
og er som det ses kun
en funktion af den tilbudte trafik og antallet af ledninger.
Når
der skal foretages beregninger med Erlangs B-formel på computere kan der være
problemer forbundet med at anvende [1]-7.34. Der sker det at tælleren hurtigt
bliver meget stor numerisk. Hvis tallet skal repræsenteres med en float eller
double i et C program, anvendes der 6 eller 15 betydende cifre iht. IEEE
standarden, samt en eksponent på ±38 eller ±308. Derfor kan
det være hensigtsmæssigt at udvikle en rekursiv metode så der undgås at regne
med store eksponenter og fakultet.
Derfor opstilles
først et udtryk for 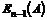
Idet
[1]-7.34 kan omskrives til følgende
og ved at indsætte ( 5-20) i ( 5-19)
fås
dette
udtryk kan omskrives til rekursionsformlen som er vist i [1]
|
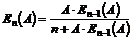
|
[1]-7.45
|
Hvor
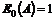 . Hermed er det muligt at regne sig frem til
. Hermed er det muligt at regne sig frem til 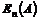 ved at starte med
ved at starte med 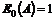 .
.
eksempel.
Den
tilbudte trafik A = 2, og der er n = 4 betjeningssteder.
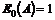
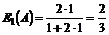
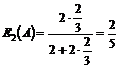
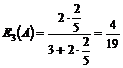
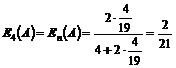
Ved
at anvende ( 5-18) får man selvfølgelig den samme værdi
for p(n)
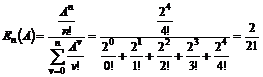
[1]-7.45 er nem at implementere i et program, f.eks. således
|
//**********************************************************
// Funktion
navn: Erlang_1
//
Parametre : (double) A = tilbudt
trafik
// (double) n = antal ledninger
// Retur
værdi : p(n) = En(A) = Erlang's
B-formel
//
Bemærkninger : Hvis funktionen convergerer mod en værdi,
// så afbrydes loopen og værdien
retuneres.
//**********************************************************
double
Erlang_1(double &A, double &n)
{
double v = 1.0; // tilstands tæller
double E = 1.0; // E0(A) = 1 pr. definition
double pE; // Tidligere værdi af E
while (v <= n)
{
pE = E;
E = pE * A / (v + A * pE);
v++;
if ((pE - E) == 0.0) // steady state er nået
break; // forlad while-løkken
}
return E;
}
|
|
Figur 5-11,
Implementering af Erlangs 1. formel i C.
|
Opkaldsspærring.
Er
den brøkdel af alle opkaldsforsøg der finder alle ledninger optaget eller
sandsynligheden for at et tilfældigt opkald bliver afvist.
Afviklet trafik.
Er
den trafik der afvikles, dvs. antallet af samtidige optagne ledninger.
|
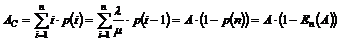
|
[1]-7.36
|
Da
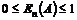 vil den afviklede
trafik altid være mindre end eller lig med den tilbudte trafik.
vil den afviklede
trafik altid være mindre end eller lig med den tilbudte trafik.
Afvist trafik.
Er
den trafik der bliver afvist, og er forskellen på den tilbudte trafik og den
afviklede trafik.
|
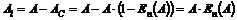
|
[1]-s142
|
Trafikspærring.
Er
den brøkdel af den tilbudte trafik der ikke afvikles. Dvs. afvist trafik i
forhold til tilbudt trafik.
Som
det ses af ( 5-18), (
5-21) og ( 5-22)
er tidsspærring = opkaldsspærring = trafikspærring.
Dette
gælder da opkaldsintensiteten er tilstandsuafhængig. Denne egenskab kaldes
PASTA-egenskaben og gælder for alle systemer med Poisson ankomstproces.
I
dette afsnit indføres et begrænset antal betjeningssteder i systemet. Først
undersøges et system med et begrænset antal betjeningssteder og et ubegrænset
antal ledninger, Poisson ankomstproces og eksponentielle betjeningstider. Hvis
nomenklaturen ventetidssystemer skal følges, vil dette system være et W/W/n
system. Men hvis man i øvrigt antager at fordelingerne er af Erlang-1 typen,
kaldes det et M/M/n system.
|
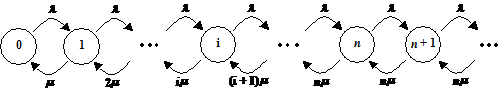
|
|
Figur 5-12, Erlangs ventetidssystem med n
betjeningssteder, et M/M/n system.
|
Tilstandsskiftintensiteter.
Den
intensitet som antal optagne ledninger skifter med kan forklares således
- Voksende antal optagne ledninger.
Da der er uendelig mange kunder, vil opkaldsintensiteten være uafhængig af hvor
mange kunder der er i systemet. Dvs. at antal optagne ledninger vokser med
konstant intensitet, nemlig opkaldsintensiteten l, der er
antal opkald pr. tidsenhed.
- Faldende antal optagne ledninger.
Når der er netop én kunde i systemet, én optaget ledning, og
middelbelægningstiden eller middelbetjeningstiden er
så vil systemet skifte fra én til nul optagne ledninger med intensiteten m, der er antal
betjente kunder pr. tidsenhed. Hvis der er to optagne ledninger, så vil
systemet skifte fra to til én optagne ledninger med den dobbelte intensitet, 2m, osv. indtil alle betjeningssteder er
optaget, i dette tilfælde er intensiteten 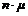 . Når der er flere kunder i systemet end der er
betjeningssteder, så vil systemet skifte til et mindre antal ledninger med
intensiteten
. Når der er flere kunder i systemet end der er
betjeningssteder, så vil systemet skifte til et mindre antal ledninger med
intensiteten 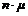 , da kunderne der ikke får betjening ikke kan forlade
systemet.
, da kunderne der ikke får betjening ikke kan forlade
systemet.
Ved at opstille
snitligninger efter samme princip som vist tidligere, kan
tilstandssandsynlighederne bestemmes. Det er vist i [1] side 274.
|
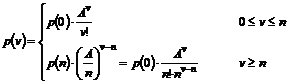
|
( 5-23)
[1]-12.2
|
Hvor 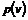 er sandsynligheden for
at v ledninger er optaget.
er sandsynligheden for
at v ledninger er optaget.
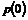 kan ligeledes
bestemmes
kan ligeledes
bestemmes
|
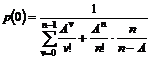
|
( 5-24)
[1]-12.4
|
En interessant
størrelse i et ventetidssystem, er sandsynligheden for at et kald kommer i kø.
Dvs. sandsynligheden for at alle betjeningssteder er optaget eller den brøkdel
af tiden som alle betjeningssteder er optaget. Denne størrelse kalden
ventetiden W.
Dette udtryk kaldes
Erlangs 2. formel eller Erlangs C-formel.
Ved at indsætte
Erlangs B-formel for 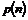 i C-formlen får man
følgende udtryk
i C-formlen får man
følgende udtryk
|
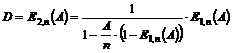
|
( 5-26)
[1]-12.7
|
Når Erlangs
B-formel er implementeret som et program, se Figur
5-11, kan Erlangs C-formel let beregnes således
|
//**********************************************************
// Funktion navn: Erlang_2
// Parametre : (double) E1 = Erlang B værdien til A og
n
// (double) A = tilbudt trafik
// (double) n = antal ledninger
// Retur værdi : E2,n(A) = Erlang's C-formel
//**********************************************************
double Erlang_2(double
&E1, double &A, double &n)
{
return E1 / (1.0 - A / n * (1.0 - E1));
}
|
|
Figur
5-13, Implementering af Erlangs 2.
formel i C.
|
Da 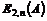 angiver
sandsynligheden for at alle betjeningssteder er optaget, så kan sandsynligheden
for at et betjeningssted er ledig udtrykkes således
angiver
sandsynligheden for at alle betjeningssteder er optaget, så kan sandsynligheden
for at et betjeningssted er ledig udtrykkes således
|
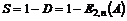
|
( 5-27)
[1]-s276
|
S
er altså sandsynligheden for at en kunde får straksbetjening.
Den afviklede
trafik findes ved at summere antal ledninger ganget med sandsynligheden for at
antallet er optaget
Da systemet har et
ubegrænset antal ledninger, bliver ingen opkald afvist, og derfor afvikles alt
den tilbudte trafik
|
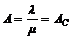
|
[1]-12.8
|
Sandsynligheden for
at finde en eller flere kunder i køen findes ved at summere sandsynlighederne
for køpladserne
|
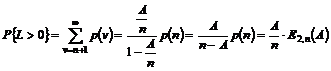
|
( 5-29)
[1]-12.9
|
hvor L er antallet af kunder i køen.
Når man er
interesseret i selve kølængden, kan der være tale om to forskellige størrelser
Middelkølængden på et vilkårligt
tidspunkt.
Middelkølængden når der er kø.
Kølængden findes
ved at trække antal betjeningssteder fra antal optagne ledninger.
Middelkølængden til et vilkårligt tidspunkt findes da ved at summere
kølængderne ganget med den respektive tilstandssandsynlighed
Hvis man benytter
at
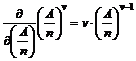
og forlænger med 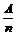
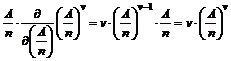
Hvis dette udtryk
indsættes i (
5-30) får man det udtryk som
findes i [1]-s278
|
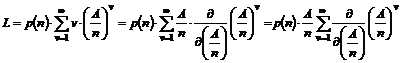
|
[1]-s278
|
For at undgå at
køen vokser mod uendeligt, skal den tilbudte trafik A være mindre end antallet af betjeningssteder n
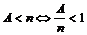
Hvis man her
udnytter rækkeudvikling som vist her
|
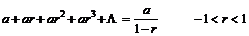
|
[6]-19.5
|
og sætter a = 1 kan udtrykket omskrives til
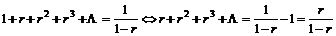
får man følgende,
idet 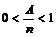
og hermed får vi
samme udtryk som vist i [1]-12.10
Idet ( 5-25) indsættes i ( 5-31) får man at
|
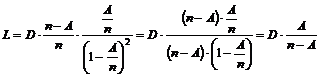
|
( 5-32)
[1]-12.10
|
Det er vigtigt at
fremhæve at denne middelkølængde er til et vilkårligt tidspunkt, altså også
selvom der ikke er kø.
Middellængden af
køen med den forudsætning at der er
kø, Lkø, er middellængden
af køen til et vilkårligt tidspunkt divideret med sandsynligheden for kø
Til de to
middelkølængder knytter der sig en middelventetid, dvs. middelkøtiden.
Middelventetiden for alle opkald, W, og middelventetiden for de opkald der
kommer i kø, w.
Fra [1] kapitel 5
haves at den gennemsnitlige kølængde er ankomstintensiteten ganget med
middelventetiden
|
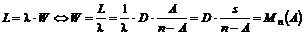
|
[1]-12.12
|
Hvor
middelbelægningstiden er
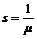 .
.
W
siger noget om hele systemets serviceniveau idet alle kunder i gennemsnit vil
opleve denne ventetid.
Derimod vil w,
middelventetiden for de kunder der er
i kø, kun opleves af de kunder der er i kø. Jo størrer denne værdi er, jo
størrer krav stilles til kundernes tålmodighed.
Fra [1]-s50 haves
umiddelbart for alle ventetidssystemer at
|
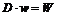
|
[1]-3.21
|
heraf
|
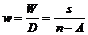
|
( 5-34)
[1]-12.14
|
I kap. 5 blev det gennemgået
hvordan man bestemmer karakteristiske størrelser for et ventetidssystem. Disse
metoder anvendes i det følgende afsnit til at karakterisere en udvidelse af
denne matematiske model. Denne udvidelse skal ske i retning af det virkelige OP118
system.
Det første der
ændres, er at antal ledninger i systemet begrænses, dvs. at der er et bestemt
antal betjeningssteder samt et begrænset antal køpladser. Derfor undersøges et
M/M/n/K/¥ system i det følgende.
M/M/n/K/¥ system.
Der antages fortsat
at ankomstprocessen er en poissonproces og belægningstiderne er
eksponentialfordelt for systemet, og der er n
betjeningssteder, K ledninger og en
uendelig stor kundepopulation. Dvs. at der er K - n køpladser i
systemet. Dette fører til følgende springintensitetsdiagram.
|

|
|
Figur 6-1,
Springintensitetsdiagram for et M/M/n/K system.
|
Da der er et
uendeligt antal kunder, vil systemet altid skifte fra en vilkårlig tilstand i til den efterfølgende tilstand i + 1 med intensiteten l når 0 £ i < K, og skift fra en vilkårlig tilstand i til den forgående tilstand i
- 1 vil ske med intensiteten im når 0 < i £ n og nm i
intervallet n £ i £ K.
( se kap. 5.2.4
).
Dette kan opstilles
på følgende måde
Snitligninger.
For senere at kunne
finde nogle udtryk der beskriver systemet, opstilles snitligningerne for
systemet vist i Figur
6-1. Dette gøres som i kap.5 for at kunne beskrive
en hvilken som helst tilstand ved 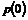 .
.
Der ønskes først et
udtryk der beskriver sandsynligheden for et vilkårligt antal telefonister er
optaget. Dette gøres ud fra snitligningerne 1 til og med n
Af ( 6-1) kan 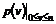 udtrykkes ved
udtrykkes ved 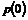 således
således
Dvs.
sandsynligheden for at netop v
betjeningssteder er optaget, når 0 £ v
£ n.
På ganske
tilsvarende måde kan snitligningerne n
+ 1 til og med K udvikles således
( 6-3) kan omskrives udtrykt ved 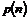 således
således
Dvs.
sandsynligheden for at netop v
ledninger er optaget, alle n
betjeningssteder er optaget og netop v
- n køpladser er optaget, når n £ v
£ K.
Ved at anvende ( 6-2) kan man få et udtryk for 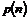 , som indsættes i (
6-4)
, som indsættes i (
6-4)
For at kunne
beregne ( 6-2) og ( 6-5)
er det nødvendigt at kende 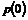 .
. 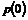 findes ved at benytte
at
findes ved at benytte
at
Indsættes ( 6-2) og ( 6-5)
i ( 6-6) får man
Det undersøges nu
om den sidste sum i nævneren på (
6-7) kan omskrives til et udtryk
der ikke indeholder summationstegn, dette gøres vha. rækkeudvikling. Først
omskrives summationen så evt. konstante værdier sættes uden for
summationstegnet.
Før end ( 6-8)
kan skrives ud, undersøges en sum af den type der indgår i dette udtryk nærmere
De to summe i ( 6-9) kan begge rækkeudvikles som vist i
[6]
|
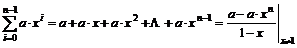
|
[6]-19.5
|
Hermed kan ( 6-9) omskrives til
Ved at anvende
denne omskrivning på ( 6-8)
fås
Man skal i ( 6-11) være opmærksom på at den tilbudte
trafik A ikke må være lig antallet af
telefonister n. Dette ville dog også
være uhensigtsmæssigt da systemet så vil blive mættet dvs. at alle nye
ankommende kunder til systemet vil blive afvist. Det er derfor en betingelse at
A / n ¹ 1 for at
systemet fungere efter hensigten.
Indsættes ( 6-12) i ( 6-7),
bliver udtrykker for 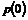
Hvor m = K
- n er antal køpladser i systemet.
Sandsynligheden for et kald kommer i kø.
Det kan i nogle
tilfælde være nødvendigt at vide hvor stor en del af kunderne der kan forventes
at komme i kø, da denne værdi kan være et udtryk for hvor godt systemet
fungere. Man kunne f.eks. forvente at hvis sandsynligheden for at komme i kø
var stor, ville ventetinden for betjening stige, hvilket hurtigt ville give
utilfredse kunder. Derimod skal der være en vis sandsynlighed for at komme i kø
for at telefonisterne udnyttes optimalt.
Sandsynligheden for
at komme i kø findes ud fra [1]-12.5 der siger at sandsynligheden for at komme
i kø er lig summen af sandsynligheder for at alle telefonister er optaget, dvs.
at tilstand K ikke medtages, for hvis
systemet er i tilstand K vil den
næste kunde blive afvist.
|
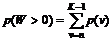
|
[1]-12.5
|
Ved at indsætte p(v) formel ( 6-5)
fås et udtryk for p(W>0)
|
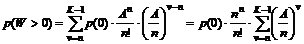
|
( 6-13)
|
Sandsynligheden for et kald får
straksbetjening.
Sandsynligheden for
et kald får straksbetjening er summen af de sandsynligheder hvor kunden ikke
bliver sat i kø og ikke bliver afvist.
Ved at indsætte p(v) formel ( 6-2)
fås et udtryk for p(W=0)
|
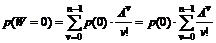
|
( 6-14)
|
Sandsynligheden for at et kald bliver afvist.
Sandsynligheden for
et kald bliver afvist er lig summen af sandsynligheder for et kald ikke får
straksbetjening eller bliver sat i kø.
|
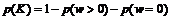
|
( 6-15)
|
Da der her kun er
tale om ét køsystem, svare sandsynligheden for et kald bliver afvist til
sandsynligheden for alle ledninger er optaget.
Hvor m = K
- n er antal køpladser i systemet.
Fremkommelighed.
Fremkommelighed er
et udtryk for hvor mange kunder der bliver betjent at det samlede antal kunder
der reelt har ringet til oplysningen. Man har dermed et udtryk for hvor
effektivt systemet er og det er netop derfor TDK bruger denne værdi til krav om
fremkommelighed. Denne værdi skal helst være så stor som mulig, TDK har sat
fremkommeligheden til at skulle være større end 0,95 i hverdagene (se Bilag 1).
Fremkommelighed er
det antal kald der enten får straksbetjening eller kommer i kø, set i forhold
til det samlede antal opkaldsforsøg.
Dette giver ved at
indsætte p(K) formel (
6-16)
|
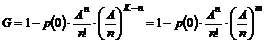
|
( 6-17)
|
Hvor m = K
- n er antal køpladser i systemet.
Middelkølængde for et vilkårligt tidspunkt.
Middelkølængden på
et vilkårligt tidspunkt er ifølge [1]-s278 et udtryk for hvor lang
køen gennemsnitligt er på et vilkårligt tidspunkt uanset om der er kø eller ej.
Se i øvrigt ( 5-30).
Ved at indsætte p(v) formel ( 6-2)
og derefter p(0) formel ( 6-7) fås et udtryk for L
Da v - n er den aktuelle køplads, omskrives
( 6-19) idet antal køpladser er m = K - n
Middelkølængde når der er kø.
Middelkølængden når
der er kø er ifølge [1]-s278 et udtryk for hvor lang køen gennemsnitligt
er i det tilfælde hvor der er kø.
Se også ( 5-33).
Ved at indsætte p(v) formel ( 6-5)
fås et udtryk for LKø
|
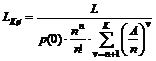
|
( 6-21)
|
Middelventetider.
Little’s sætning
siger at den gennemsnitlige kølængde er lig ankomstintensiteten gange
middelventetiden. Se [1]-s279.
Hvor W er
middelventetiden for alle opkald dvs. et udtryk for den tid der går før en
kunde kan forvente betjening. Ved at isolere W fås
Dvs. at
middelventetiden er bestemt af kølængden på et vilkårligt tidspunkt og den
trafikintensitet der ankommer til systemet.
Da L allerede er
kendt fås det endelige udtryk for middelventetiden for hele systemet
( 6-22) kan ligesom ( 6-20) udtrykkes ved antal køpladser m
|
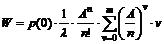
|
( 6-23)
|
I dette kapitel
blev der udviklet en matematisk model for et M/M/n/K system. Der er dog visse
forudsætninger for at denne model kan anvendes.
1.
Ankomstprocessen
er en poissonproces.
2.
Betjeningstiderne
er eksponentialfordelte.
3.
Der
skal være stationaritet / statistisk ligevægt, dvs. at alle parametre er
uafhængige af det absolutte tidspunkt.
4.
Kundepopulationen
er uendelig.
5.
Kunderne
må ikke kunne forlade systemet uden betjening.
Ad 1 og 2.
Det har ikke været
muligt at efterprøve om ankomstprocessen er en poissonproces eller om
betjeningstiderne er eksponentialfordelte. Men det er nødvendige antagelser for
at kunne anvende den klassiske teletrafikteori.
Ad 3.
Da der kun er
statistisk ligevægt når alle parametre er konstante, skal systemet betragtes i
et tidsinterval hvor man har en konstant opkaldsintensitet l og konstant middelbetjeningstid s, således at m tillige er konstant. Det kan lade sig gøre
ved at anvende de statiske data der indsamles for OP118 til at fastslå i hvilke
intervaller disse parametre kan antages konstante. Det gøres typisk ved at
inddele døgnet i intervaller på en time.
Ad 4.
Kundepopulationen
antages for uendelig stor, hvilket selvfølgelig ikke passer.
Hvis man regner med
en endelig kundepopulation P, får det
indflydelse på hvordan springintensitetsdiagrammet vist i Figur 6-1 skifter til den næste tilstand.
Tilstandsskiftene vil da ske med på følgende måde
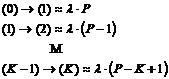
Hvis P >> K vil der ikke være nævneværdig forskel på de intensiteter systemet
skifter tilstand med. Og dermed kan intensiteterne betragtes som værende
konstante, ligesom i et system med en uendelig kundepopulation.
Ad 5.
Der er ikke taget
højde for at kunder kan forlade systemet uden at have fået betjening, dvs. at
kunden ikke selv kan afbryde forbindelsen mens han/hun er i kø, og kunden kan
ikke blive nedkoblet pga. timeout, se kap.3.3.
I OP118 systemet er
det netop muligt at nedkoble en kunde inden betjening og det er også muligt for
kunden selv at afbryde forbindelsen ved at lægge røret på. Denne problematik er
behandlet i litteraturen, se [1] kap.12.8, hvor man betragter tilstandsskiftintensiteterne
på følgende måde
Hvor mr angiver den intensitet utålmodig kunder og kunder
der bliver nedkoblet pga. timeout o.l. forlader køen med. Det er særdeles
vanskeligt at bestemme mr, hvorfor denne problematik ikke er behandlet i
denne rapport.
Dette kapitel
indfører overløbsproblematikken, som er beskrevet nærmere i kap.3.8, og en matematisk
model for den ene af -dsa centralerne opstilles. Der er n telefonister og de skal fortsat betjene kunderne tilhørende denne
central. Populationen er ubegrænset og ankomstprocessen antages at være en
poissonproces med opkaldsintensiteten l1 og betjeningstiderne at være eksponentialfordelte
med middelbetjeningstiden
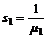 .
.
De kunder der
afvises fra den anden central pga. fyldt demandqueue antages tillige at ankomme
efter en poissonproces med opkaldsintensiteten l2 og betjeningstiderne at være
eksponentialfordelte med middelbetjeningstiden
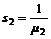 .
.
Dvs. at der er to
trafiktyper, almindelige kunder og overløbs kunder.
I Figur 6-2 er det vist hvordan systemet ser ud
med overløb medtaget.
Da begge
trafiktyper skal have den samme betjening, antages det at
middelbetjeningstiderne for trafiktyperne er ens
Da begge
trafiktyper ankommer efter en poissonproces, vil de sammenlagt ankomme efter en
poissonproces med intensiteten
Det antages altså
at trafiktype 2 (overløbskunder) ankommer efter en poissonproces. Dette kan
måske være tvivlsom, da der kun er overløbstrafik når køen er fyldt på den
anden central. Man kan derfor forestille sig at overløbstrafikken kommer i
perioder, og når overløbstrafikken er der, antages den at ankomme efter en
poissonproces.
Systemet kan nu
simplificeres til følgende
|
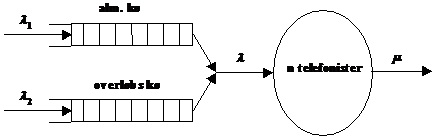
|
|
Figur
6-3 Simplificeret system når l = l1 + l2.
|
Det kan dermed
antages at telefonisterne modtager en trafik med intensiteten l og afvikler denne trafik med intensiteten m som vist her
|
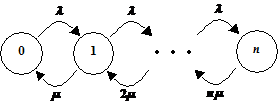
|
|
Figur
6-4 Springintensitetsdiagram for n betjeningssteder.
|
De to trafiktyper
har ikke nødvendigvis den samme opkaldsintensitet, da man kan forvente at
overløbskunderne ankommer med en mindre intensitet end de almindelige kunder.
Derfor bliver de to køer ikke fyldt og afviklet med de samme intensiteter, men
med trafiktypernes respektive intensiteter. Da de to køer bliver afviklet i
tilfældig orden, dvs. at begge køer kan være helt eller delvis fyldte på samme
tid, så skal den ene kø kunne skifte til en kunde mere eller mindre i køen
medens den anden kø indeholder et vilkårligt antal kunder eller er tom. Disse
krav opfyldes ved følgende springintensitetsdiagram
|
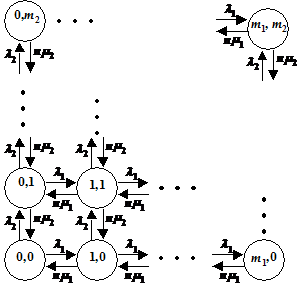
|
|
Figur 6-5
Springintensitetsdiagram for to køsystemer.
|
Der betragtes her
et todimensionalt køsystem med forskellig l og m som i Figur
6-5 hvor tilstand m1 er antallet af køpladser
for trafiktype 1, og m2 er
antallet af køpladser for trafiktype 2. Da springintensitetsdiagrammet er i to
dimensioner refereres tilstandene som (i,
j), hvor i er antal trafiktype 1 kunder i kø og j er antal trafiktype 2 kunder i kø. Som det ses, bliver type 1
køen behandlet med intensiteterne l1 og nm1, og type 2 køen med l2 og nm2 altså efter samme princip som kap.6.1.
Hvis der ikke er
nogen cirkulationsflow i dette diagram, så er processen reversibel. Dvs. at
hvis man betragter fire tilstande så skal flowet med uret være det samme som
flowet mod uret
|
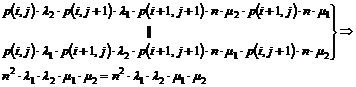
|
[1]-10.10
[1]-10.11
|
Som det ses, er
kravet om reversibilitet opfyldt i dette tilfælde, og derfor er der lokal
balance. At der lokal balance betyder at man kan lægge et snit mellem to
vilkårlige tilstande og opstille sædvanlige snitligninger, f.eks. vil et snit
mellem tilstande (i, j) og (i + 1, j) give
|
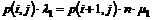
|
[1]-12.12
|
Ved at betragte
snitligningerne mellem to tilstande der ikke er nabotilstande, f.eks. (a,b)
og (c,d), hvor a < c og b < d, kan man opstille nogle generelle
udtryk. Figur
6-6 er en skitse over vejen mellem
de to tilstande.
|
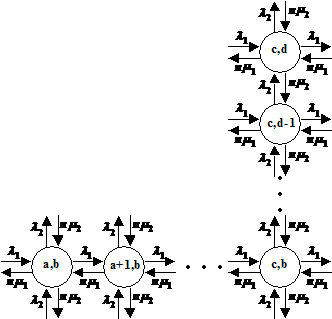
|
|
Figur 6-6, Vejen
mellem to vilkårlige tilstande.
|
Alle snitligninger
i den vandrette del af vejen fra (a,b) til (c,d), dvs. fra (a,b)
til (c,b)
Af ovenstående får
vi udtrykket
|
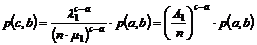
|
( 6-24)
|
Hvor A1 er den tilbudte type 1
trafik.
Og snitligningerne
i den lodrette del af vejen fra (a,b) til (c,d), dvs. fra (c,b)
til (c,d)
Af ovenstående får
vi udtrykket
|
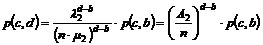
|
( 6-25)
|
Hvor A2 er den tilbudte type 2
trafik.
Nu kan 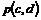 beskrives ved
beskrives ved 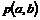
Dvs. at en
vilkårlig tilstand i køen 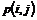 kan udtrykkes ved
kan udtrykkes ved 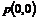 ved at sætte
ved at sætte 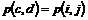 og
og 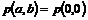
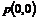 er tilstanden lige før
en kunde kan komme i en af de to køer, dvs. at alle n telefonister netop er optaget. Derfor får vi at
er tilstanden lige før
en kunde kan komme i en af de to køer, dvs. at alle n telefonister netop er optaget. Derfor får vi at
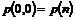
og ( 6-26) bliver nu
Dvs.
sandsynligheden for en vilkårlig kombination af type 1 og type 2 køpladser
optaget.
Bemærk at netop 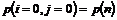 , altså at når alle n
telefonister netop er optaget vil den næst kunde blive sat i kø.
, altså at når alle n
telefonister netop er optaget vil den næst kunde blive sat i kø.
Dvs. at tilstand n og (0,0) er identiske og som tidligere
antages betjeningstiderne ens.
Derfor kan
springintensitetsdiagrammet nu vises således
|
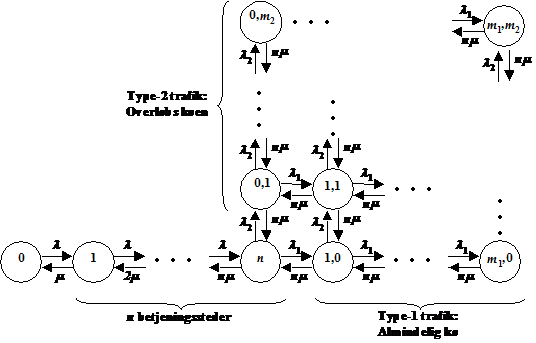
|
|
Figur 6-7,
Springintensitetsdiagram for et M/M/n/(m1,m2) system
|
Figurforklaring
n antal
telefonister
m1 antal
køpladser for almindelig trafik
m2 antal
køpladser for overløbstrafik
l1 den
opkaldsintensitet som almindelig trafik ankommer med
l2 den
opkaldsintensitet som overløbs trafik ankommer med
l den
opkaldsintensitet telefonisterne belægges med: 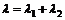
m den intensitet telefonisterne betjener
kunderne med: m = m1 = m2
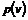 kan bestemmes ganske
som i kap.5.2.7
formel ( 5-16) ved at betragte snitligningerne
fra tilstand 0 til tilstand n, og man
får da
kan bestemmes ganske
som i kap.5.2.7
formel ( 5-16) ved at betragte snitligningerne
fra tilstand 0 til tilstand n, og man
får da
Dvs.
sandsynligheden for at netop alle betjeningssteder er optaget.
2
Og A er den samlede tilbudte trafik
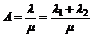
Som det ses, er 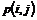 afhængig af
afhængig af 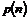 der igen er afhængig
af
der igen er afhængig
af 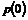 . Derfor bestemmes
. Derfor bestemmes 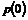 i det følgende.
i det følgende.
Idet det udnyttes
at summen af alle tilstandssandsynligheder skal være 1, får man
Dobbeltsummen er
summen af alle køtilstandssandsynligheder inklusive 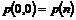 , og denne sum undersøges nærmere
, og denne sum undersøges nærmere
Idet [6]-19.5
anvendes, får man følgende
Som det ses, er det
en forudsætning at A1 ¹ n og A2
¹ n.
Ved at udtrykke p(n)
( 6-29) ved p(0) fås
Dette udtryk
indsættes i (
6-30) og 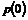 kan nu bestemmes
kan nu bestemmes
|
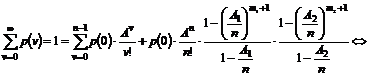
|
|
|
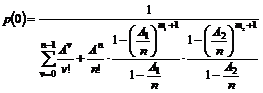
|
( 6-31)
|
Sandsynligheden for et vilkårligt kald kommer
i kø.
Sandsynligheden for
et kald kommer i kø er sandsynligheden for at et kald af trafiktype 1 eller 2
ikke får straksbetjening. Dvs. en summation af de sandsynligheder hvor en kunde
ikke får straksbetjening, dette kan skrives på følgende måde.
Det skal bemærkes
at summationen kun går til mx
- 1. Dette skyldes at tilstandene p(m1,0) ... p(m1,
m2) og p(0,m2)
... p(m1, m2)
er sandsynligheder for at et kald bliver afvist. Sandsynligheden for at blive
afvist vil blive beskrevet senere.
Dette giver ved at
indsætte p(i , j), formel (
6-27).
Vha. ( 6-29) kan p(W > 0) udtrykkes med
p(0) i stedet for p(n)
|
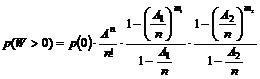
|
( 6-32)
|
Da
trafikintensiteten består af to intensiteter vil sandsynligheden for de enkelte
trafiktyper kommer i kø være følgende
Sandsynligheden for et trafiktype 1 kald
kommer i kø.
Da der kun ønskes
sandsynligheder tilhørende trafiktype 1 fås følgende summation
p(i , j), formel ( 6-27)
indsættes i udtrykket.
Vha. ( 6-29) kan p(W1 > 0) udtrykkes med p(0) i stedet for p(n)
Ved at udnytte
rækkeudvikling ( se formel [6]-19.5 ) fås
|
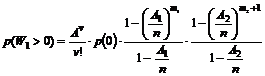
|
( 6-33)
|
Sandsynligheden for et trafiktype 2 kald
kommer i kø.
Dette giver ved at
indsætte p(i , j), formel (
6-27).
Vha. ( 6-29) kan p(W2 > 0) udtrykkes med p(0) i stedet for p(n)
Ved at udnytte
rækkeudvikling ( se formel [6]-19.5 ) fås
|
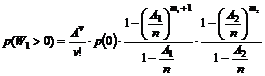
|
( 6-34)
|
Sandsynligheden for et kald får
straksbetjening.
Sandsynligheden for
en kunde får straksbetjening er lig sandsynligheden for en kunde ikke bliver
sat i kø. Dette kan udtrykkes på følgende måde
Ved at indsætte p(v),
formel ( 6-28) fås
|
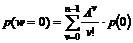
|
( 6-35)
|
Sandsynligheden for at et kald bliver afvist.
Sandsynligheden for
et kald bliver afvist er lig sandsynligheden for et kald at type 1 eller 2 ikke
får straksbetjening og ikke bliver sat i kø. Det skal dog bemærkes at når type
1 trafik afvises, vil trafikken overgå til den anden central som type 2 trafik
(overløb). Men i dette projekt betragtes overløbstrafik som afvist trafik, da
overløbstrafik er et udtryk for at den pågældende central afvikler trafikken
dårligt.
Sandsynligheden for
at et kald bliver afvist kan udtrykkes med følgende ligning
|
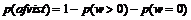
|
( 6-36)
|
Man kan også
betragte det som summen af de tilstande hvor et kald bliver afvist
Vha. ( 6-27) indsættes p(i , m2) og p(m1
, j) hvilket giver
p(n) kan udtrykkes ved p(0), se ( 6-29),
hvilket giver
Ved at udnytte
rækkeudvikling ( se [6]-19.5 ) fås
Fremkommelighed.
Fremkommelighed er
del af kunderne der enten får straksbetjening eller kommer i kø, set i forhold
til det samlede antal opkaldsforsøg.
Dette giver ved at
indsætte p(afvist) formel (
6-37).
|
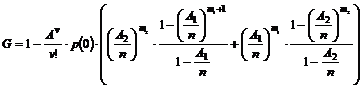
|
( 6-38)
|
Middelkølængde for et vilkårligt tidspunkt.
Da der findes to
køer i systemet opdeles middelkølængden i henholdsvis trafiktype 1 og
trafiktype 2. Som grundmodel anvendes dog stadig den samme formel som i kap. 6.1.
Trafiktype 1.
Først opstilles en
formel for trafiktype 1 hvor de tilstande summeres hvor kunden ikke får
straksbetjening. Dette giver jævnfør (
6-18)
Ved at opstille
summen og ved at anvende (
6-27) og ( 6-28)
fås
Ved at udnytte
rækkeudvikling ( se [6]-19.5 ) fås
|
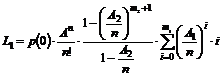
|
( 6-39)
|
Trafiktype 2.
Formlen for
trafiktype 2 opstille som for trafiktype 1 hvilket giver
Ved at opstille
summen og ved at anvende (
6-27) ( 6-28)
fås
Ved at udnytte
rækkeudvikling ( se [6]-19.5 ) fås
|
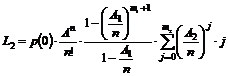
|
( 6-40)
|
Middelkølængde når der er kø.
Da det drejer sig
om to køtyper vil hver kø have deres middelkølængde. Der kan opstilles følgende
udtryk jævnfør [1].
Trafiktype 1.
Ved at indsætte ( 6-27) og ( 6-28)
og rækkeudvikle, se [6]-9.15, får man udtrykket
|
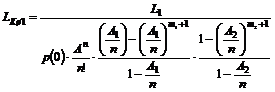
|
( 6-41)
|
Trafiktype 1.
Ved at indsætte ( 6-27) og ( 6-28)
og rækkeudvikle, se [6]-9.15, får man udtrykket
|
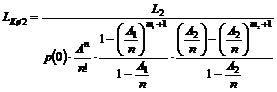
|
( 6-42)
|
Middelventetider.
Middelventetiden
for alle opkald kunne ifølge kap.6.1
beskrives som forholdet mellem kølængden på et vilkårligt tidspunkt i forhold
til trafikintensiteten.
Da middelventetiden
er afhængig af begge køtyper må
Ved at indsætte
udtrykkene for L1 og L2 fås
|
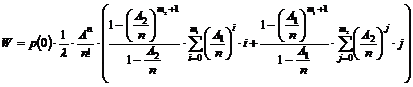
|
( 6-43)
|
I dette kapitel
blev der udviklet en matematisk model for et M/M/n/(m1,m2)
system. Der er dog visse forudsætninger for at denne model kan anvendes.
1.
Ankomstprocessen
er en poissonproces.
2.
Betjeningstiderne
er eksponentialfordelte.
3.
Der
skal være stationaritet / statistisk ligevægt, dvs. at alle parametre er
uafhængige af det absolutte tidspunkt.
4.
Kundepopulationen
er uendelig.
5.
Kunderne
må ikke kunne forlade systemet uden betjening.
6.
Ad 1,
overløbskunderne skal også ankomme efter en poissonproces.
7.
Almindelige
kunder og overløbskunder skal have samme middelbetjeningstider som begge skal
være eksponentialfordelte.
Punkterne 1 til og
med 5 er de samme som der blev foretaget i kap. 6.1.1, hvor disse forudsætninger er
kommenteret.
Ad 6.
Det forventes at
overløbskunderne ankommer i intervaller, hvorfor ankomstprocessen kun vil være
en poissonproces i disse intervaller og ikke gennem en længere periode. Derfor
gælder den matematiske model kun i de intervaller hvor der er overløbskunder
eller i de intervaller hvor der ikke er overløbskunder. I tilfældet af at der
ikke er overløbskunder viser det sig at et M/M/n/(m1,m2)
vil være identisk med et M/M/n/K system, se kap.6.3.
Ad 7.
Da begge typer
kunder skal have samme betjening kan det antages at kunderne har samme
middelbetjeningstider og tidsfordelingstype.
For at kunne
konkludere hvilken betydning det får for systemet at man indfører overløb,
sammenlignes de karakteristiske størrelser for de to systemer.
For de to systemer
er følgende udtryk for p(0) fundet
|
M/M/n/K
|
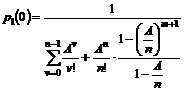
|
|
M/M/n/(m1,m2)
|
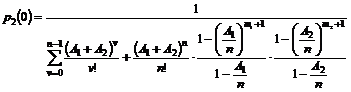
|
For de to systemer
er følgende udtryk for fremkommeligheden G
fundet
|
M/M/n/K
|
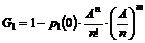
|
|
M/M/n/(m1,m2)
|
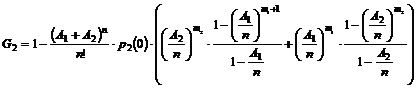
|
For de to systemer
er følgende udtryk for ventetiden W
fundet
|
M/M/n/K
|
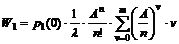
|
|
M/M/n/(m1,m2)
|
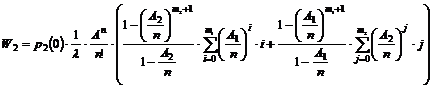
|
Som det ses, vil
udtrykkene for M/M/n/(m1,m2) systemet være identisk med
udtrykkene for M/M/n/K systemet under følgende forudsætninger
1.
A2
for M/M/n/(m1,m2) systemet skal være lig 0, A2 = 0.
2.
m1
for M/M/n/(m1,m2) systemet skal være lig m for M/M/n/K systemet, m1 = m.
3.
A1
for M/M/n/(m1,m2) systemet skal være lig A for M/M/n/K systemet, A1 = A.
4.
n for M/M/n/(m1,m2) systemet skal være lig n for M/M/n/K systemet, n = n.
Der fremgår tillige
af Figur 6-7 at hvis man “skærer” trafik type 2
køpladserne væk, vil systemet være identisk med det på Figur 6-1.
Under alle andre
omstændigheder er de to systemer forskellige, og forskellen undersøges i det
følgende.
Det undersøges nu
hvilken indflydelse de ekstra led i p2(0)
har når p1(0) og p2(0) skal sammenlignes
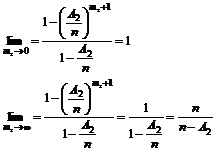
Da A2 < n vil dette led altid være større end 1.
Derudover gælder at 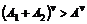 under den forudsætning at A1 = A.
under den forudsætning at A1 = A.
Dvs. at nævneren i p2(0) vil være større end
nævneren i p1(0) og dermed
fås at
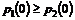
Hvilket vil sige at
der i et M/M/n/(m1,m2) system er mindre sandsynlighed for
at alle telefonister er ledige end i et M/M/n/K system. Dette lyder fornuftigt,
under den forudsætning at der tilbydes mest trafik til M/M/n/(m1,m2)
systemet.
At p2(0) < p1(0) vil bidrage til en
bedre fremkommelighed, men ved at betragte de ekstra led i G2 ses det disse vil bidrage til en ringere
fremkommelighed. Men da en sammenligning af G1
og G2 involverer mange
ubekendte, er det ikke muligt at beskrive en sammenhæng mellem disse.
En vigtig vurdering
er at sørge for at fremkommeligheden for M/M/n/(m1,m2)
systemet er mindst lige så godt som fremkommeligheden for M/M/n/K systemet da
fremkommeligheden naturligvis skal være i overensstemmelse med TDK’s målsætning
om fremkommelighed. Det involverer at man skal tilpasse antal betjeningssteder,
n, og antallet af de to typer
køpladser, m1 og m2. Det har ikke været muligt
at løse dette problem matematisk, men der er udviklet et simuleringsværktøj med
hvilken det er muligt at løse disse problemer, se kap. 6.4.
I kap. 6.2 indeholder
udtrykkene for de forskellige tilstandssandsynligheder mange ubekendte, derfor
kan det være meget besværligt at løse udtrykkene mht. en eller flere af de
ubekendte. Dvs. at når det skal vurderes om TDK’s målsætninger mht.
fremkommelighed osv. er opfyldte, så er disse vurderinger afhængige af mange
parametre. Derfor udvikles der en metode til at simulere OP118 systemet med
overløb i dette kapitel. Dette simuleringsværktøj udformes som et program
skrevet i C. Ved at udnytte at der er lokal balance overalt i systemet, kan en
iterativ algoritme opstilles der ikke indeholder eksponenter eller fakulteter,
og dermed bliver der ikke problemer med meget store tal.
I det foregående
kapitel fremgik det, at alle tilstandssandsynlighederne kan udtrykkes ved p(0). Det kan gøres ved at udnytte, at
der overalt i springintensitetsdiagrammet er lokal balance. Ved at lade p(0) være 1, kan alle andre
tilstandssandsynlighederne let beregnes, men tilstandssandsynlighederne er
selvfølgelig forkerte nu, da summen af alle sandsynligheder skal være 1.
Tilstandssandsynlighederne denormeres derfor ved at bestemme summen af alle tilstandssandsynligheder
og derefter dividere de enkelte tilstandssandsynlighederne med denne sum.
Princippet belyses bedst ved at vise et eksempel.
Eksempel.
I et M/M/n/(m1,m2)
system med poisson ankomstproces og eksponentialfordelte tidsintervaller har
man følgende oplysninger
Der er 4
betjeningssteder, 3 køpladser til type 1 trafik og 2 køpladser til type 2
trafik. Opkaldsintensiteten for trafiktype 1 er 1 og 2 for trafiktype 2.
Middelbetjeningstiden er 0,25 og er ens for de to trafiktyper
l1 = 1
l2 = 2
m = 4
n
= 4
m1
= 3
m2
= 2
Betjeningsstederne
oplever en samlet opkaldsintensitet
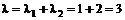
Den samlede
tilbudte trafik og de to trafiktypers tilbudte trafik kan nu beregnes
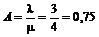
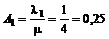
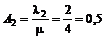
Springintensitetsdiagrammet
for systemet kan vises således
|

|
|
Figur 6-8, Et
eksempel på et M/M/n/(m1,m2) system
|
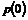 sættes til 1
sættes til 1
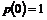
Tilstandssandsynlighederne
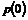 til og med
til og med 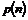 beregnes ud fra den
betragtning at der skal være lokal balance
beregnes ud fra den
betragtning at der skal være lokal balance
|
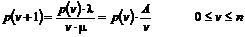
|
( 6-44)
|
Som det ses, undgås
fakultet og store eksponenter, så problemet med overflow eksisterer ikke her!
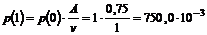
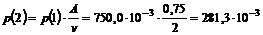
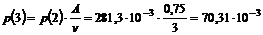
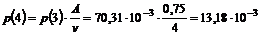
Da der også er
lokal balance i køsystemet, kan vi opstille følgende to udtryk
Da 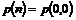 kan
kan 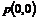 til
til 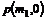 bestemmes vha. ( 6-45)
bestemmes vha. ( 6-45)
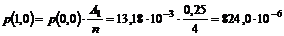
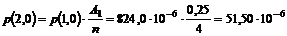
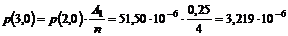
Med kendskab til 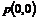 til
til 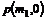 kan
kan 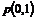 til
til 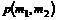 bestemmes vha. ( 6-46)
bestemmes vha. ( 6-46)
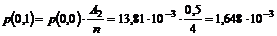
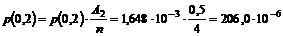
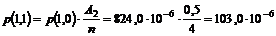
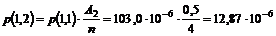
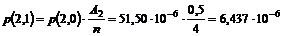
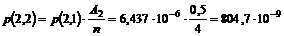
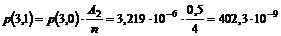
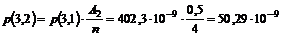
Iht. Figur 6-8 er tilstandssandsynlighederne nu
|
|
|
|
|
206,0e-6
|
12,87e-6
|
804,7e-9
|
50,29e-9
|
|
|
|
|
|
1,648e-3
|
103,0e-6
|
6,437e-6
|
402,3e-9
|
|
1,000
|
750e-3
|
281,3e-3
|
70,31e-3
|
13,18e-3
|
824,0e-6
|
51,50e-6
|
3,219e-6
|
Summen af alle
tilstandssandsynligheder bliver
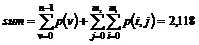
Alle
tilstandssandsynligheder normaliseres nu ved at dividere dem med sum, og vi får da følgende
|
|
|
|
|
97,28e-6
|
6,080e-6
|
380,0e-9
|
23,75e-9
|
|
|
|
|
|
778,2e-6
|
48,64e-6
|
3,040e-6
|
190,0e-9
|
|
472,2e-3
|
354,2e-3
|
132,8e-3
|
33,20e-3
|
6,226e-3
|
389,1e-6
|
24,32e-6
|
1,520e-6
|
Ved kontrol viser
det sig som forventet, at summen af alle tilstandssandsynligheder er 1
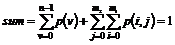
Sandsynligheden for
at et kald kommer i kø er summen af de sandsynligheder, hvor næste tilstand er
i køen.
Sandsynligheden for
at et trafik type 1 kald kommer i kø er da jf. kap.6.2
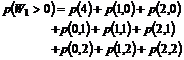
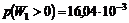
Tilsvarende får vi
sandsynligheden for at en trafiktype 2 kald kommer i kø
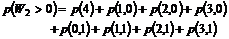
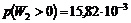
Og sandsynligheden
for at et vilkårligt opkald kommer i kø bliver
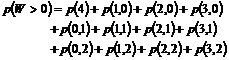
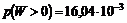
Da der kun er
anvendt tre betydende cifre i eksemplet, ser det ud til at 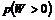 er det samme som
er det samme som 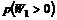 , hvilket ikke er tilfældet.
, hvilket ikke er tilfældet.
Sandsynligheden for
at et kald bliver afvist er
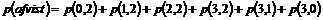
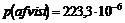
Fremkommeligheden
er
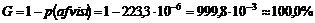
De øvrige parametre
som er omtalt i 6.2
lader sig tilsvarende let beregne, når tilstandssandsynlighederne er beregnet.
For at kunne
sammenligne de to systemer, M/M/n/K og M/M/n/(m1,m2), er
der blevet skrevet et program, SIMUL.CPP, der kan foretage numeriske
beregninger på et M/M/n/(m1,m2) system.
Programmets
anvendelse er kun, at give en forståelse for hvilken indflydelse forskellige
parameterændringer vil give på et system. Samt at kunne optimere antal
betjeningssteder (n), type 1 eller
type 2 køpladser (m1 eller
m2), således at et givet
fremkommelighedskrav netop er opfyldt.
Det skal være
muligt at indlæse følgende parametre til beskrivelse af et M/M/n/(m1,m2)
system.
A1 Tilbudt
type 1 trafik.
A2 Tilbudt
type 2 trafik.
n Antal
betjeningssteder.
s Middelbetjeningstid.
m1 Antal
type 1 køpladser.
m1 Antal
type 1 køpladser.
G Fremkommelighedskrav.
navn Navn
på datafil.
Programmet skal
kunne foretage følgende.
-
Indlæse
/ ændre på trafikparameterne
-
Beregne
tilstandssandsynlighederne og gemme disse i en tekstfil, se formatet på denne
fil i det følgende afsnit.
-
Optimere
antal betjeningssteder således at fremkommelighedskravet netop er opfyldt.
-
Optimere
antal type 1 køpladser således at fremkommelighedskravet netop er opfyldt.
-
Optimere
antal type 2 køpladser således at fremkommelighedskravet netop er opfyldt.
Rutediagrammet vist
i Figur 6-9 viser strukturen i programmet.
Programmet er skrevet i programmeringssproget C og er vedlagt i bilag 5, og på
disketten i bilag 6.
Programmet
beskrives ikke i sin helhed, men de væsentlige funktioner beskrives kort i det
følgende.
Det har været
nødvendigt at indføre matricer i beregningerne, derfor er der defineret en ny
type der består af et 2 dimensionalt array af typen double. Funktionen til at
allokere RAM til disse matricer er taget fra [7].
Funktionen MMnm1m2.
Til beregning af
tilstandssandsynligheder er funktionen MMnm1m2 skrevet. Denne funktion beregner
tilstandssandsynlighederne ud fra den tilbudte trafik A1 og A2,
antal betjeningssteder n, antal type 1 køpladser m1 og antal type 2 køpladser
m2. Funktionen returnerer tilstandssandsynlighederne i to matricer
der tillige overføres til funktionen. En 1-dimensional matrice til
tilstandssandsynlighederne p(0) til og med p(n), samt en 2-dimensional matrice
til p(0,0) til og med p(m1,m2).
MMnm1m2 beregner
tilstandssandsynlighederne efter samme princip som vist i kap.6.4.1.
Funktionen TDK Krav.
Til beregning af
fremkommelighed, middelkølængde og middelventetid er funktionen TDKKrav
skrevet. Denne funktion beregner disse værdier efter samme princip som vist i
kap.6.4.1.
Funktionen optimer_n_m1_m2.
Denne funktion kan
optimere antal betjeningssteder, type 1 kølængde eller type 2 kølængde således
at krav om fremkommelighed netop er opfyldt. Det gøres ved først at beregne den
aktuelle fremkommelighed. Hvis den aktuelle fremkommelighed er for lille, så
forøges n, m1 eller m2
med én, eller formindskes der med én. Denne procedure fortsættes indtil
fremkommeligheden netop er opfyldt.
Data fil format
Programmet kan
udskrive en beskrivelse af systemet, samt alle tilstandssandsynligheder til en
tekst fil. Data bliver skrevet således, hvor [TAB] betyder adskillelse med
tabulator, “Abc” betyder at der skrives teksten Abc og udtryk i kursiv betyder
at selve talværdien skrives.
“A=” [TAB] A
“A1=” [TAB] A1
“A2=” [TAB] A2
“n=” [TAB] n
“m1=” [TAB] m1
“m2=” [TAB] m2
p(0)
p(1)
.
.
.
p(n) [TAB] p(1,0) [TAB] p(2,0) [TAB] ... p(m1,0)
p(0,1) [TAB] p(1,1) [TAB] p(2,1) [TAB] ... p(m1,1)
. . . .
. . . .
. . . .
p(0,m2) [TAB] p(1,
m2) [TAB] p(2, m2) [TAB] ... p(m1, m2)
I figuren herunder
er det vist et eksempel på en data fil.
|
A= 11.0000
A1= 10.0000
A2= 1.0000
n= 8
m1= 5
m2= 2
0.0000
0.0001
0.0008
0.0029
0.0079
0.0175
0.0320
0.0503
0.0692
0.0692 0.0865 0.1081 0.1351 0.1689 0.2111
0.0086 0.0108 0.0135 0.0169 0.0211 0.0264
0.0011 0.0014 0.0017 0.0021 0.0026 0.0033
|
|
Figur
6-10, Eksempel på en data fil.
|
Eksempel på anvendelse af SIMUL.CPP.
I det følgende
undersøges det, hvor mange telefonister og køpladser der er nødvendig i et
M/M/n/K system for netop at opfylde TDK’s krav om fremkommelighed og svartid.
Derefter undersøges et M/M/n/(m1,m2) system, hvor det
antages, at når der er overløbstrafik, så er denne trafik den halve intensitet
som type 1 trafikken.
M/M/n/K system.
TDK siger at
fremkommeligheden skal være bedre end 95% og at svartiden højst må være 15 sek.
Den tilbudte trafik A = A1 sættes til 100, antal
telefonister n sættes til 120 og
kølængden m1 sættes til
50. Middelbetjeningstiden sættes i dette eksempel til 1 tidsenhed.
Når programmet
startes op, vil man blive præsenteret for følgende skærmbillede
|
M/M/n/(m1,m2) - OP118 systemet med overløb -
SIMULATOR
Brian
Eilschou Märcher / Rudi Bjørn Rasmussen
----------------------------------------------------------------------
Tilbudt trafik type 1 : A1 = 0.0000
Tilbudt trafik type 2 : A2 = 0.0000
Tilbudt total trafik : A
= 0.0000
Middelbetjeningstid : s
= 0.0000
Antal betjeningssteder: n = 50
Antal type 1 køpladser: m1 = 25
Antal type 2 køpladser: m2 = 90
Aktuel fremkommelighed: af = 0.0000
Fremkommeligheds krav : fk = 0.0000
Middelkølængde :
L = 0.0000
Aktuel ventetid : aW = 0.0000
Ventetidskrav krav : Wk = 0.0000
Datafil : f = test.txt
----------------------------------------------------------------------
[1]
Indlæs nye parametre
[2]
Beregn tilstandssandsynligheder og gem i datafil
[3]
Beregn n ud fra et fremkommelighedskrav
[4] Beregn m1 ud fra et
fremkommelighedskrav
[5]
Beregn m2 ud fra et fremkommelighedskrav
[0]
Afslutter programmet
|
Nu skal der
indtastet parametre der beskriver systemet.
Ved at trykke på 1,
skifter skærmbilledet til input menuen der ser således ud
|
M/M/n/(m1,m2) - OP118 systemet med overløb -
SIMULATOR
Brian
Eilschou Märcher / Rudi Bjørn Rasmussen
----------------------------------------------------------------------
[1]
Tilbudt trafik type 1 : A1 = 0.0000
[2]
Tilbudt trafik type 2 : A2 = 0.0000
[3]
Middelbetjeningstid : s = 0.0000
[4] Antal
betjeningssteder: n = 50
[5] Antal
type 1 køpladser: m1 = 25
[6] Antal
type 2 køpladser: m2 = 90
[7]
Fremkommeligheds krav : fk = 0.0000
[8]
Datafil : f = test.txt
[0] Afslut
parameter indtastning
----------------------------------------------------------------------
Hvilken parameter skal ændres:
|
Nu sættes de
forskellige parametre.
Tast 1 Þ Indtast tilbudt trafik type 1 : A1 = 100 [ENTER]
Tast 2 Þ Indtast tilbudt trafik type 2 : A2 = 0 [ENTER]
Tast 3 Þ Indtast middelbetjeningstid : s = 1 [ENTER]
Tast 4 Þ Indtast antal betjeningssteder : n = 120 [ENTER]
Tast 5 Þ Indtast antal trafik type 1 køpladser : m1
= 50 [ENTER]
Tast 6 Þ Indtast antal trafik type 2 køpladser : m2
= 1 [ENTER]
Tast 7 Þ Indtast fremkommelighedskrav : fk = 0.95 [ENTER]
BEMÆRK: For at
programmet virker efter hensigten, så skal m1
og m2 sættes til mindst 1
køplads. For at simulere et M/M/n/K system skal en af de tilbudte trafikke blot
være 0, i dette tilfælde sættes A2
= 0.
Tast 0 for at gå
tilbage til menuen.
Bemærk at netop når
der ikke er nogen trafik type 2 køpladser, så svarer M/M/n/(m1,m2)
systemet til et M/M/n/K system.
Tilstandssandsynlighederne
og fremkommeligheden for det aktuelle system bliver nu beregnet, og
skærmbilledet ser nu ud således
|
M/M/n/(m1,m2) - OP118 systemet med overløb -
SIMULATOR
Brian
Eilschou Märcher / Rudi Bjørn Rasmussen
-------------------------------------------------------------
Tilbudt trafik type 1 : A1 = 100.0000
Tilbudt trafik type 2 : A2 = 0.0000
Tilbudt total trafik : A
= 100.0000
Middelbetjeningstid : s
= 1.0000
Antal betjeningssteder: n = 120
Antal type 1 køpladser: m1 = 50
Antal type 2 køpladser: m2 = 1
Aktuel fremkommelighed: af = 1.0000
Fremkommeligheds krav : fk = 0.9500
Middelkølængde :
L = 0.1658
Aktuel ventetid : aW = 0.0017
Ventetidskrav krav : Wk = 0.0000
Datafil : f = test.txt
-------------------------------------------------------------
[1] Indlæs nye parametre
[2]
Beregn tilstandssandsynligheder og gem i datafil
[3]
Beregn n ud fra et fremkommelighedskrav
[4]
Beregn m1 ud fra et fremkommelighedskrav
[5]
Beregn m2 ud fra et fremkommelighedskrav
[0]
Afslutter programmet
|
Som det ses, så er
fremkommeligheden 100%, dvs. at fremkommeligheden godt kan gøres mindre, det
gøres ved at optimere systemet mht. antal betjeningssteder ved at trykke på 3,
hvilket resulterer i at følgende besked bliver vist nederst på skærmen
c = 96 -> fremk. = 0.9566
Det betyder at ved
at reducere antal betjeningssteder til 96, er fremkommeligheden 95,66% stadig
væk opfyldt. Nu optimeres der mht. antal køpladser ved at trykke på 4, hvilket
resulterer i følgende besked
c = 28 -> fremk. = 0.9504
Dvs. at antal
køpladser kan reduceres til 28, således at fremkommeligheden er 95,04%
Det fremgår desuden
at svartiden nu er 14,45% af middelbetjeningstiden. Af TDK’s statistik
materiale fremgår det, at for OP118 tjenesten er betjeningstiden typisk 45
sek., hvilket medfører en svartid på ca. 6 sek. hvilket er OK i forhold til
TDK’s krav.
Dvs. at i et
M/M/96/28 system med en tilbudt trafik A
= 100 vil TDK’s krav til fremkommelighed og svartider netop være opfyldte.
M/M/n/(m1,m2) system.
Den tilbudte trafik
A1 sættes til 100 som før og A2
sættes til 50, antal telefonister n
sættes til 96 og kølængderne m1
og m2 sættes begge til 50.
Middelbetjeningstiden sættes igen til 1 tidsenhed.
Der optimeres først
mht. type 1 køpladser og derefter mht. type 2 køpladser hvilket resulterer i et
M/M/99/(38,12) system med en fremkommelighed på ca. 95% og en svartid på ca. 7
sek.
Hvis der først
optimeres mht. type 2 køpladser og derefter mht. type 1 køpladser vil det
resulterer i et M/M/99/(44,8) system med en fremkommelighed på ca. 95% og en
svartid på ca. 9 sek.
Delkonklusion.
Som det fremgår af
eksemplerne, er det muligt ved simulering at beregne antal telefonister, type 1
og 2 køpladser, således at et fremkommelighedskrav netop er opfyldt. Så hvis
man er i stand til at bestemme værdierne for de tilbudte trafiker samt
middelbetjeningstiden, er det simpelt at bestemme de øvrige parametre.
Der er i dette
projekt forsøgt at foretage en analyse af en servicetelefoncentral. Dette er
gjort ved først at beskrive GLAD systemet for derefter at foretage en
statistisk- og matematisk analyse.
GLAD systemet.
Det kan på
nuværende tidspunkt konkluderes, at beskrivelsen af GLAD systemet har taget
længere tid end forventet (se bilag 3). Dette skyldes, at vi ikke på forhånd
havde kendskab til GLAD systemet og da det materiale vi havde til rådighed (
[2] og [3] ), er af en sådan art, at det på forhånd kræver kendskab til
systemet. Det skyldes tillige, at det har været nødvendigt at interviewe forskellige
TDK medarbejdere for at få svar på spørgsmål og begreber, som ikke klart
fremgik af disse materialer.
Men vi mener dog,
at det udarbejdede kapitel om GLAD systemet, er særdeles velegnet til at
introducere systemet for læseren. Derudover kan kapitlet anvendes til at give
nyansatte hos TDK, et indblik i GLAD systemets opbygning.
For vores
vedkommende har det været nødvendigt at gennemgå GLAD systemet detaljeret, for
senere at kunne udarbejde et detaljeret tilstandsdiagram, for et kalds mulige
skæbner i OP118 systemet. Dette tilstandsdiagram har været nødvendigt for det
videre arbejde omhandlende statistik.
Statistik.
Der er ud fra
tilstandsdiagrammet blevet udarbejdet et endeligt forslag til en
statistikopsamling, hvor forslaget er en kombination af TDK’s og den forslåede
statistik.
I udarbejdelsen
af vores forslag til en
statistikopsamling, blev det på forhånd bestemt ikke at studere TDK’s
statistikopsamling. Dette blev gjort, for at kunne give et selvstændig og mere
objektiv forslag til en statistikopsamling. Ved senere sammenligning af de to
statistikopsamlinger viste det sig at de havde meget til fælles, men der var
også nogle ting i den forslåede statistikopsamling som TDK ikke havde med og
omvendt. Der blev derfor udarbejdet et endeligt forslag til en
statistikopsamling der består af en kombination af TDK’s og den af os
forslåede.
Der er dog en ting
der ikke er blevet taget højde for i den forslåede statistikopsamling, nemlig
hvor vidt det er muligt at realisere disse målinger, hvilket indbefatter
målemetoder og måleteknikker. Der er dog i projektet nævnt et par simple
målemetoder, men disse kræver en grundigere gennemgang, da der her ikke er
taget hensyn til de usikkerhedder der er forbundet med disse målemetoder.
Hvis det viser sig
at det kan lade sig gøre at realisere målingerne, mener vi at have forbedret
TDK’s statistik opsamlinger, da man i den endelige statistikopsamling får et
mere nuanceret billede over hvor effektiv OP118 systemet er. Dette kan
begrundes med at den forslåede statistik giver et mere detaljeret overblik over
hvad der sker i systemet, herunder lokalisering af svage områder i systemet,
eller et overblik over hvor mange kunder der enten bliver nedkoblet eller selv
afbryder forbindelsen og hvor denne nedkobling foregår.
Teletrafik
Da vi på forhånd
ikke havde kendskab til teletrafikteori, har det været nødvendigt at først
studere denne teori, inden det har været muligt at lave matematiske modeller
over OP118 systemet. For at læsere uden kendskab til teletrafikteori skal kunne
læse rapporten, har det været nødvendigt at skrive et afsnit der kort
introducerer grundbegreberne, samt de områder af teletrafikteorien der senere
anvendes til udvikling af de matematiske modeller.
Herefter er det
lykkedes at udvikle først en simpel model (M/M/n/K) for derefter at udvide
denne model i retning af den virkelige OP118 tjeneste (M/M/n/(m1,m2)).
Det har vist sig
endog særdeles vanskeligt at foretage sammenligninger af de to modeller, samt
at dimensionere antal betjeningssteder, n,
og køpladser, m1 og m2, således at TDK’s
målsætninger er opfyldte. Derfor er der blevet udviklet et program, der kan
foretage numeriske beregninger på et M/M/n/(m1,m2)
system, samt optimere mht. fremkommelighedskrav. Med dette program er det
muligt at dimensionere antal telefonister, samt at dimensionere de to
køstørrelser så systemets fremkommelighed opfylder et på forhånd givet krav.
Den matematiske
model er dog ikke fuldstændig tilpasset OP118 tjenesten, da der er ikke taget
hensyn til at kunder kan forlade køen før betjening. Desuden skal der for at få
et komplet overblik udvikles en matematisk model der indeholder både khdsa og
kddsa, da overløbstrafikken forbinder de to centraler. Der ud over er dette
projekt fokuseret på OP118 tjenesten, men servicetelefonen har mange andre
tjenester, der hver især har sin opkaldsintensitet, middelbetjeningstid og
kølængde. Desuden er Recall queue heller ikke medtaget i den matematiske model.
Generelt om dette
projekt kan der siges at det har været meget teoretisk, hvormed menes at der
ikke er blevet udviklet en konkret ting. Dette er meget usædvanligt for
projekter på Odense Teknikum, og er derfor heller ikke noget vi har prøvet før.
Projektets omfang
var også for stort i forhold til den tid der var til rådighed. Man kunne derfor
have begrænset projektet til at omhandle enten statistik eller teletrafikteori.
At projektets omfang var stort var kendt på forhånd og det blev derfor kun
forventet at projektet skulle munde ud i et fundament for en viderebearbejdning
af de stillede opgaver.
Dette mener vi også
at have opnået, da der i statistikdelen stadig er mulighed for at undersøge
hvordan opsamlinger realiseres, samt en videre bearbejdning og analyse af de
opsamlede data. Derudover se vi rig mulighed for at videreudvikle de i kap.6
udarbejde matematiske modeller for køsystemer, både med hensyn til flere
trafiktyper og med hensyn til nedkobling af kunder. For os at se ligger de
største muligheder, til at beskrive trafiksystemer, i at udvikle programmer der
kan simulerer disse matematiske modeller, da det ikke er muligt, ud fra de
opstillede udtryk alene, at overskue de enkelte parametres indvirkning på
systemet.
Bilag 1.
Fremkommeligheds krav.
TDK har opstillet følgende målsætninger til
OP118 tjenesten.
Fremkommelighed.
|
Periode
|
Definition
|
Mål
|
|
Mandag – fredag 0800-1700
|
Gennemsnit
pr. måned af antal opkald i forhold til antal opkaldsforsøg.
|
> 95 %
|
|
|
Antal
timer pr. måned hvor fremkommeligheden er lavere end 90%.
|
0 timer
|
|
Mandag-fredag 1700-0800 samt lørdag,
søndag og helligdage hele døgnet.
|
Gennemsnit
pr. måned af antal besvarede opkald i forhold til antal opkaldsforsøg.
|
> 90%
|
Svartid.
|
Periode
|
Definition
|
Mål
|
|
Mandag – fredag 0800-1700
|
Gennemsnit pr. måned af den tid der går
før OP-kald besvares.
|
<15 sek.
|
|
Mandag-fredag 1700-0800 samt lørdag,
søndag og helligdage hele døgnet.
|
Gennemsnit pr. måned af den tid der går
før OP-kald besvares.
|
<25 sek.
|
Træfsikkerhed.
|
Periode
|
Definition
|
Mål
|
|
Hele døgnet.
|
Antallet af korrekte svar i forhold til
det samlede antal forespørgsler.
|
> 98 %
|
Bilag 2.
Forkortelser.
AIP Advanced
Intelligent Peripheral.
ASN Advanced
Service Node.
AXE digital
telefoncentral.
CC Call
Completion.
CCITT No 7 Comité
Consulatif International Télégraphique et Téléphonique. Anvendes ikke mere, se
ITU-T system 7.
CRIMP talemaskine.
DB Data
Base or other application.
DRC Distributed
ressource controller.
ESS Extended
Switching Subsystem.
FMS File
Management Subsystem.
GLAD Gain
LAndsdækkende Danmark
GW GateWay.
HW Hardware.
IN Intelligent
Network.
INAP Intelligent
Networks Application Part.
INph2.1 Intelligent
Network, se IN.
IPUP Intelligent
Peripheral User Part.
ISUP ISDN
User Part.
Kddsa Kolding
digital special central.
Khdsa København
digitale special central.
LC Local
Central.
MCS Man-machine
Communication Subsystem.
MT Maintenance
Terminal.
O&M Operation
& Maintenance.
OMS Operation
and Maintenance Subsystem.
OP-database OPlysnings
- database.
OPS Operator
Subsystem.
OPUP OPerator
User Part.
ORD Kald
type: ORDinary call type. Almindelig opkald.
OSI Open
System Interconnection.
OTN Operater
Terminal Network (Token Ring).
PNO Public
Network Operator.
PRM ProtokolReferenceModel.
PSTN Public
Switched Telephone Network.
RSF Resource
Switching Control.
SCF Service
Control Function.
SCP Service
Control Point (INph2.1).
SMAS Service
Management Application System.
SOF Service
Operator Functions.
SP Service
Provider.
SSCP Service
Switching and Control Point.
SSF Service
Switching Function.
SSP Service
Switching Point (INph2.1).
TCAP Transaction
Capability Application Part.
TCP/IP Transmission
Control Protocol / Internet Protocol.
TCS Traffic
Control Subsystem.
TUP Telephone
User Part.
TV-database Telefon
Vagt - database.
WS Work
Station.
Bilag 3.
Tidsplan.
Forløbig tidsplan.
|
Uge
|
36
|
37
|
38
|
39
|
40
|
41
|
42
|
43
|
44
|
45
|
46
|
47
|
48
|
49
|
|
Overblik
|
x
|
x
|
o
|
|
|
|
|
|
|
|
|
|
|
|
|
Beskrivelse af GLAD systemet
|
|
|
x
|
x
|
x
|
|
|
|
|
|
|
|
|
|
|
Problemstilling
|
|
o
|
x
|
x
|
|
|
|
|
|
|
|
|
|
|
|
Studie af teletrafik
|
|
|
x
|
x
|
x
|
x
|
|
|
|
|
|
|
|
|
|
Analyse
og af statistik
|
|
|
|
|
x
|
x
|
x
|
o
|
|
|
|
|
|
|
|
Opstilling af mat. modeller
|
|
|
|
|
|
|
o
|
x
|
x
|
x
|
o
|
|
|
|
|
Raportskrivning
|
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
x: prioriteret.
o: ikke
prioriteret.
Realiserede tidsplan.
|
Uge
|
36
|
37
|
38
|
39
|
40
|
41
|
42
|
43
|
44
|
45
|
46
|
47
|
48
|
49
|
|
Overblik
|
x
|
x
|
x
|
x
|
x
|
o
|
x
|
|
|
|
|
|
|
|
|
Beskrivelse af GLAD systemet
|
|
|
x
|
x
|
x
|
x
|
x
|
x
|
o
|
|
|
|
|
|
|
Problemstilling
|
|
o
|
x
|
x
|
o
|
|
|
|
|
|
|
|
|
|
|
Studie af teletrafik
|
|
|
x
|
x
|
x
|
o
|
o
|
x
|
x
|
x
|
|
|
|
|
|
Analyse
og af statistik
|
|
|
|
|
|
o
|
x
|
x
|
x
|
x
|
o
|
|
|
|
|
Opstilling af mat. modeller
|
|
|
|
|
|
|
|
o
|
o
|
x
|
x
|
x
|
x
|
|
|
Raportskrivning
|
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x: prioriteret.
o: ikke
prioriteret.
Bilag 4.
Litteratur
henvisninger.
[1] Teletrafik Teori, Villy Bæk Iversen.
[2] AXE 10, OPS AND OTN Survey, EN/LZBD 202
32.
[3] AXE OPS - Operator Assistance in the
Public Network, Product Description.
[4] Advanced Engineering Mathematics, Erwin
Kreyszig, 7. Edition, ISBN 0-471-59989-1.
[5] OSI Protokolreferencemodellen, Claus
Vaarning, ISSN 0105-8541 Rapport IT-125, Januar 1991.
[6] Schaum’s “Mathematical Handbook of
Formulas and Tables”, ISBN 0-07-060224-7.
[7] Beginning with C, Ron House, ISBN
0-534-94122-2.
Interviewede personer.
{1} Claus Vaarning, TDK, Klingenberg.
{2} Dorte Madsen, TDK STS, Klingenberg.
Bilag 5.
Programudskrift.
|
#include <iostream.h>
#include <dos.h>
#include <conio.h>
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <string.h>
#define outxy(x,y,t) gotoxy(x,y); printf(t)
///////////////////////////////////////////////////////////////////
// MATRIX funktioner
herunder
// sakset fra
"beginning with C, Ron House, ISBN 0-534-94122-2
typedef double **matrix;
matrix mat_create(int row, int column)
{
double *elements, **rows;
int i;
elements =
(double*)malloc(row*column*sizeof(double));
if (elements ==
NULL) return NULL;
rows =
(double**)malloc(row*sizeof(double));
if (rows == NULL)
return NULL;
for (i = 0; i <
row; i++)
rows[i] =
&elements[column*i];
return rows;
}
// sakset fra
"beginning with C, Ron House, ISBN 0-534-94122-2
// MATRIX funktioner
herover
///////////////////////////////////////////////////////////////////
//**********************************************************
// Funktion
navn: besked
// Parametre : char
*besked
// Bem‘rkninger : viser en besked nederst p† sk‘rmen
//**********************************************************
void besked(const char *besked)
{
gotoxy(1,24);
cout <<
besked;
}
//**********************************************************
// Funktion navn: gem_data
// Parametre :
ingen
// Bem‘rkning :
gemmer tilstandssandsynligheder i en fil
//**********************************************************
void gem_data(const char* fnavn, \
double &A,
double &A1, double &A2, \
int &n, int
&m1, int &m2, \
matrix
&p0_n, matrix &p00_m1m2)
{
// t‘llere
int i, j;
// udskriv til en
data-fil
FILE *outf =
fopen(fnavn, "w+t");
// skriv info i
starten af filen
fprintf(outf,
"A=\t\t%-16.4f\n", A);
fprintf(outf,
"A1=\t\t%-16.4f\n", A1);
fprintf(outf,
"A2=\t\t%-16.4f\n", A2);
fprintf(outf,
"n=\t\t%4d\n", n);
fprintf(outf,
"m1=\t\t%4d\n", m1);
fprintf(outf,
"m2=\t\t%4d\n", m2);
for (i = 0; i <=
n; i++)
fprintf(outf,
"%-16.4f\n", p0_n[i][0]);
for (j = 0; j <=
m2; j++)
{
for (i = 0; i
<= m1; i++)
fprintf(outf,
"%-16.4f\t", p00_m1m2[i][j]);
fprintf(outf,
"\n");
}
fclose(outf);
}
//**********************************************************
// Funktion navn: MMnm1m2
// Parametre :
A: tilbudt trafik total, dvs til telefoonisterne
// A1: tilbudt
type 1 trafik
// A2: tilbudt
type 2 trafik
// n: antal
betjeningssteder
// m1: antal
type 1 kø pladser
// m2: antal
type 2 kø pladser
// p0_n: betjeningsstedernes tilstandssandsynligheder
// p00_m1m2: tilstandssandsynlighederne i 2-dim k› system
// Bem‘rkninger: Denne funktion beregner
tilstandssandsynlighederne i et
// M/M/n/(m1,m2)
system, og retunerer disse i de to matricer.
//**********************************************************
void MMnm1m2(double &A, double &A1, double
&A2, \
int &n, int
&m1, int& m2, \
matrix
&p0_n, matrix &p00_m1m2
)
{
// tællere
int i, j;
// summen af alle tilstandssanssynligheder
double sum;
// p(0) sættes til 1
p0_n[0][0] =
(double) 1.0;
sum = p0_n[0][0];
// beregn p(1) til
og med p(n)
for (i = 1; i <=
n; i++)
{
p0_n[i][0] =
p0_n[i - 1][0] * A / (double) i;
sum +=
p0_n[i][0];
}
// p(0,0) = p(n)
p00_m1m2[0][0] =
p0_n[n][0];
// beregn A1 / n, reducerer
processorbelastningen
double q = A1 /
(double) n;
// beregn p(1,0)
til og med p(m1,0)
for (i = 1; i <=
m1; i++)
{
p00_m1m2[i][0] =
p00_m1m2[i-1][0] * q;
sum +=
p00_m1m2[i][0];
}
// beregn A2 / n, reducerer
processorbelastningen
q = A2 / (double)
n;
for (i = 0; i <=
m1; i++)
// beregn p(i,1) til og med p(i,m2)
for (j = 1; j
<= m2; j++)
{
p00_m1m2[i][j] =
p00_m1m2[i][j - 1] * q;
sum +=
p00_m1m2[i][j];
}
// alle tilstandssandsynlighederne normaliseres
nu
// ved at dividere med sum
for (i = 0; i <=
n; i++)
p0_n[i][0] /=
sum;
for (i = 0; i <=
m1; i++)
for (j = 0; j
<= m2; j++)
p00_m1m2[i][j]
/= sum;
}
//**********************************************************
// Funktion navn: TDKKrav
// Parametre : p00m1m2: tilstandssandsynlighederne
i 2-dim kø system
// m1, m2: matricens dimensioner
// Bem‘rkninger : Beregner fremkommelighed og
middelk›l‘ngde, disse
// retuneres
i fk og kl
//**********************************************************
void TDKKrav(double &A, double &A1, double
&A2, double &s, \
int
&n, int &m1, int &m2, \
matrix
&p00m1m2, \
double
&fk, double &kl, double &W)
{
// tællere
int i, j;
// summen af de aktuelle tilstande
double sum = 0.0;
/////////////////////////////////////////////
// fremkommelighed beregnes
// summer p(0,m2) til og med p(m1,m2)
for (i = 0; i <=
m1; i++)
sum +=
p00m1m2[i][m2];
// sumer p(m1,0) til og med p(m1,m2-1)
// p(m1,m2) skal IKKE tælles med to gange!
for (j = 0; j <
m2; j++)
sum +=
p00m1m2[m1][j];
fk = (double) 1.0 -
sum;
/////////////////////////////////////////////
// middelk›l‘ngde beregnes
kl = 0.0;
for (i = 0; i <=
m1; i++)
for (j = 0; j
<= m2; j++)
kl +=
p00m1m2[i][j] * ((double) i + (double) j);
/////////////////////////////////////////////
// middelventetiden beregnes
W = kl * s / A;
}
//**********************************************************
// Funktion navn: input
// Bemærkninger : indlæser diverse parametre
//**********************************************************
void input(double &A, double &A1, double &A2,
double &s, double &fk, \
int &n, int
&m1, int& m2, char *f)
{
int p, y;
char buf[256];
do
{
y = 1;
clrscr();
outxy( 1,
y++," M/M/n/(m1,m2) - OP118
systemet med overløb - SIMULATOR");
outxy( 1,
y++," Brian Eilschou Marcher /
Rudi Bjørn Rasmussen");
outxy( 1, y++,
"----------------------------------------------------------------------");
sprintf(buf,
"[1] Tilbudt trafik type 1 : A1 =
%-16.4f", A1);
outxy( 1, y++,
buf);
sprintf(buf,
"[2] Tilbudt trafik type 2 : A2 =
%-16.4f", A2);
outxy( 1, y++,
buf);
sprintf(buf,
"[3] Middelbetjeningstid : s
= %-16.4f", s);
outxy( 1, y++,
buf);
sprintf(buf,
"[4] Antal betjeningssteder: n = %d", n);
outxy( 1, y++,
buf);
sprintf(buf,
"[5] Antal type 1 køpladser: m1 =
%d", m1);
outxy( 1, y++,
buf);
sprintf(buf,
"[6] Antal type 2 køpladser: m2 =
%d", m2);
outxy( 1, y++,
buf);
sprintf(buf,
"[7] Fremkommeligheds krav : fk =
%-16.4f", fk);
outxy( 1, y++,
buf);
sprintf(buf,
"[8] Datafil : f = %s", f);
outxy( 1, y++,
buf);
outxy( 1, y++,
"[0] Afslut parameter
indtastning");
outxy( 1, y++,
"----------------------------------------------------------------------");
outxy( 1, y++,
"Hvilken parameter skal ‘ndres: ");
p = getch();
switch (p)
{
case '1':
cout
<< "\nIndtast tilbudt trafik type 1 : A1 = ";
cin
>> A1;
A = A1 +
A2;
break;
case '2':
cout
<< "\nIndtast tilbudt trafik type 2 : A2 = ";
cin
>> A2;
A = A1 +
A2;
break;
case '3':
cout
<< "\nIndtast middelbetjeningstid : s = ";
cin
>> s;
break;
case '4':
cout
<< "\nIndtast antal betjeningssteder : n = ";
cin
>> n;
break;
case '5':
cout
<< "\nIndtast antal trafik type 1 køpladser: m_1 = ";
cin
>> m1;
break;
case '6':
cout
<< "\nIndtast antal trafik type 2 køpladser: m_2 = ";
cin
>> m2;
break;
case '7':
cout
<< "\nIndtast fremkommelighedskrav : fk = ";
cin
>> fk;
break;
case '8':
cout
<< "\nIndtast output fil navn : fn = ";
cin
>> f;
break;
}
} while (p != '0');
while (kbhit()) p =
getch();
}
//**********************************************************
// Funktion navn: menu
// Bemærkninger : viser menuen og retunerer på brugerens
respons
//**********************************************************
int menu(double A, double A1, double A2, double s, \
double fkrav,
double fakt, \
double Wkrav,
double Wakt, double L, \
int n, int m1,
int m2, const char *fn)
{
char buf[256];
int y = 1;
clrscr();
outxy( 1,
y++," M/M/n/(m1,m2) - OP118
systemet med overløb - SIMULATOR");
outxy( 1,
y++," Brian Eilschou Marcher /
Rudi Bjørn Rasmussen");
outxy( 1, y++,
"----------------------------------------------------------------------");
sprintf(buf,
"Tilbudt trafik type 1 : A1 = %-16.4f", A1);
outxy( 1, y++,
buf);
sprintf(buf,
"Tilbudt trafik type 2 : A2 = %-16.4f", A2);
outxy( 1, y++,
buf);
sprintf(buf,
"Tilbudt total trafik : A = %-16.4f", A);
outxy( 1, y++,
buf);
sprintf(buf,
"Middelbetjeningstid : s = %-16.4f", s);
outxy( 1, y++,
buf);
sprintf(buf,
"Antal betjeningssteder: n =
%d", n);
outxy( 1, y++, buf);
sprintf(buf,
"Antal type 1 køpladser: m1 = %d", m1);
outxy( 1, y++,
buf);
sprintf(buf,
"Antal type 2 køpladser: m2 = %d", m2);
outxy( 1, y++,
buf);
sprintf(buf,
"Aktuel fremkommelighed: af = %-16.4f", fakt);
outxy( 1, y++,
buf);
sprintf(buf,
"Fremkommeligheds krav : fk = %-16.4f", fkrav);
outxy( 1, y++,
buf);
sprintf(buf,
"Middelk›l‘ngde : L = %-16.4f", L);
outxy( 1, y++,
buf);
sprintf(buf,
"Aktuel ventetid : aW =
%-16.4f", Wakt);
outxy( 1, y++,
buf);
sprintf(buf,
"Ventetidskrav krav : Wk =
%-16.4f", Wkrav);
outxy( 1, y++,
buf);
sprintf(buf,
"Datafil : f = %s", fn);
outxy( 1, y++,
buf);
outxy( 1, y++,
"----------------------------------------------------------------------");
outxy( 1, y++,
"[1] Indlæs nye
parametre");
outxy( 1, y++,
"[2] Beregn
tilstandssandsynligheder og gem i datafil");
outxy( 1, y++,
"[3] Beregn n ud fra et
fremkommelighedskrav");
outxy( 1, y++,
"[4] Beregn m1 ud fra et
fremkommelighedskrav");
outxy( 1, y++,
"[5] Beregn m2 ud fra et
fremkommelighedskrav");
outxy( 1, y++,
"[0] Afslutter
programmet");
while (!kbhit());
return getch();
}
//**********************************************************
// Funktion
navn: optimer_n_m1_m2
// Bemærkninger : finder den n eller m1 eller m2 hvor
//
fremkommelighedskravet netop er opfyldt
// z = 0
=> n
// z = 1
=> m1
//
z = 2 => m2
// Retur
v‘rdi : retunerer 1 hvis en v‘rdi bliver funder, ellers
0
//
n vil indehode ny v‘rdi og matricerne er opdateret
//**********************************************************
int optimer_n_m1_m2(int z, \
double
&A, double &A1, double &A2, double &s, \
double
&fkrav, double &faktuel, \
double
Wkrav, double &Wakt, double &L, \
int &n,
int &m1, int &m2, \
matrix
&p0n, matrix &p00m1m2)
{
char buf[256];
int sgn = 0;
int rv = 0;
int gammel; // hvis
funktionen fejler, retuneres samme v‘rdi
int *c; //
peger p† den v‘rdi der ‘ndres
switch (z)
{
case 0: c =
&n; break;
case 1: c =
&m1; break;
case 2: c =
&m2; break;
}
gammel = *c;
// beregn tilstandssandsynlighederne
MMnm1m2(A, A1, A2,
n, m1, m2, p0n, p00m1m2);
// bestem den aktuelle fremkommelighed
TDKKrav(A, A1, A2,
s, n, m1, m2, p00m1m2, faktuel, L, Wakt);
// hvis den er for lille, så tæl op
if (faktuel <
fkrav)
sgn = 1;
else
sgn = -1;
do
{
// tæl antal op med 1
*c += sgn;
sprintf(buf,
"c = %d
", *c);
besked(buf);
// frigør den eksisterende telefonist matrice
// eller k› matricen
// og alloker ny plads
if (z == 0)
{
free(*p0n);
free(p0n);
// alloker RAM til telefonist matricen
p0n =
mat_create(*c+1,1);
}
else
{
free(*p00m1m2);
free(p00m1m2);
// alloker RAM til k› matricen
switch (z)
{
case 1: p00m1m2
= mat_create(*c+1,m2+1); break;
case 2: p00m1m2
= mat_create(m1+1,*c+1); break;
}
}
// vis en eventuel fejl
if ((p0n == NULL)
|| (p00m1m2 == NULL))
{
besked("\n\nFEJL:
ikke nok hukommelse");
while
(!kbhit());
// alloker RAM til telefonist matricen
// eller k›
switch (z)
{
case 0:
n = gammel;
p0n =
mat_create(n+1,1);
break;
case 1:
m1 = gammel;
p00m1m2 =
mat_create(m1+1,m2+1);
break;
case 2:
m2 = gammel;
p00m1m2 =
mat_create(m1+1,m2+1);
break;
}
return 0;
}
// beregn tilstandssandsynlighederne
switch (z)
{
case 0:
MMnm1m2(A,
A1, A2, *c, m1, m2, p0n, p00m1m2);
TDKKrav(A,
A1, A2, s, *c, m1, m2, p00m1m2, faktuel, L, Wakt);
break;
case 1:
MMnm1m2(A,
A1, A2, n, *c, m2, p0n, p00m1m2);
TDKKrav(A,
A1, A2, s, n, *c, m2, p00m1m2, faktuel, L, Wakt);
break;
case 2:
MMnm1m2(A,
A1, A2, n, m1, *c, p0n, p00m1m2);
TDKKrav(A,
A1, A2, s, n, m1, *c, p00m1m2, faktuel, L, Wakt);
break;
}
sprintf(buf,
"c = %d -> fremk. = %-16.4f", *c, faktuel);
besked(buf);
} while (sgn == 1 ?
faktuel < fkrav : faktuel >= fkrav);
// hvis der blev talt nedad, så gå en opad
if (sgn == -1)
{
(*c)++;
if (z == 0)
{
free(*p0n);
free(p0n);
// alloker RAM til telefonist matricen
p0n =
mat_create(*c+1,1);
}
else
{
free(*p00m1m2);
free(p00m1m2);
// alloker RAM til k› matricen
switch (z)
{
case 1: p00m1m2
= mat_create(*c+1,m2+1); break;
case 2: p00m1m2
= mat_create(m1+1,*c+1); break;
}
}
// vis en eventuel fejl
if ((p0n == NULL)
|| (p00m1m2 == NULL))
{
besked("\n\nFEJL:
ikke nok hukommelse");
while
(!kbhit());
// alloker RAM til telefonist matricen
// eller k›
switch (z)
{
case 0:
n = gammel;
p0n =
mat_create(n+1,1);
break;
case 1:
m1 = gammel;
p00m1m2 =
mat_create(m1+1,m2+1);
break;
case 2:
m2 = gammel;
p00m1m2 =
mat_create(m1+1,m2+1);
break;
}
return 0;
}
// beregn tilstandssandsynlighederne
MMnm1m2(A, A1,
A2, n, m1, m2, p0n, p00m1m2);
TDKKrav(A, A1,
A2, s, n, m1, m2, p00m1m2, faktuel, L, Wakt);
sprintf(buf,
"c = %d -> fremk. = %-16.4f", *c, faktuel);
besked(buf);
}
return 1;
}
void main()
{
double A, A1 = 10.0, A2 = 1.0, s = 1.0;
A = A1 + A2;
double faktuel = 0.0;
double fkrav = 0.95;
double L = 0.0; // middelk›l‘ngden
double Waktuel = 0.0; //
aktuel middel ventetid for ALLE kunder
double Wkrav = 0.0; // krav om middel ventetid for ALLE kunder
int n = 8, m1 = 5, m2 = 2;
matrix p0n;
matrix p00m1m2;
char fn[256]; strcpy(fn, "test.txt");
int tast;
char data_inde = 0x00; // 1 når systemdata
er indlæst
data_inde = 0x01;
// alloker RAM til matrixene
p0n =
mat_create(n+1,1);
p00m1m2 =
mat_create(m1+1,m2+1);
// vis en eventuel fejl
if ((p0n == NULL)
|| (p00m1m2 == NULL))
{
besked("\n\nFEJL:
ikke nok hukommelse");
while (!kbhit());
exit(1);
}
// beregn tilstandssandsynlighederne
MMnm1m2(A, A1, A2,
n, m1, m2, p0n, p00m1m2);
// bestem den aktuelle fremkommelighed
TDKKrav(A, A1, A2,
s, n, m1, m2, p00m1m2, faktuel, L, Waktuel);
do
{
tast = menu(A,
A1, A2, s, fkrav, faktuel, Wkrav, Waktuel, L, n, m1, m2, fn);
switch (tast)
{
case '1':
{
// frigør de eksisterende matricer
if
(data_inde)
{
free(*p0n);
free(p0n);
free(*p00m1m2);
free(p00m1m2);
}
// indlæs nye data
input(A,
A1, A2, s, fkrav, n, m1, m2, fn);
data_inde =
0x01;
// alloker RAM til matrixene
p0n =
mat_create(n+1,1);
p00m1m2 =
mat_create(m1+1,m2+1);
// vis
en eventuel fejl
if ((p0n ==
NULL) || (p00m1m2 == NULL))
{
besked("\n\nFEJL:
ikke nok hukommelse");
while
(!kbhit());
exit(1);
}
// beregn tilstandssandsynlighederne
MMnm1m2(A,
A1, A2, n, m1, m2, p0n, p00m1m2);
// bestem den aktuelle fremkommelighed
TDKKrav(A,
A1, A2, s, n, m1, m2, p00m1m2, faktuel, L, Waktuel);
}
break;
case '2':
{
if
(data_inde)
{
// beregn tilstandssandsynlighederne
MMnm1m2(A,
A1, A2, n, m1, m2, p0n, p00m1m2);
// bestem den aktuelle fremkommelighed
TDKKrav(A,
A1, A2, s, n, m1, m2, p00m1m2, faktuel, L, Waktuel);
// gem systemdata og tilstandssandsynlighederne
gem_data(fn,
A, A1, A2, n, m1, m2, p0n, p00m1m2);
besked("OK:
tilstandssandsynlighederne er beregnet og gemt");
while
(!kbhit());
}
else
{
besked("FEJL:
du skal indtaste systemdata inden beregninger");
while
(!kbhit());
}
}
break;
case '3':
{
if
(data_inde)
{
optimer_n_m1_m2(0,
A, A1, A2, s, fkrav, faktuel, Wkrav, Waktuel, L, n, m1, m2, p0n, p00m1m2);
while
(!kbhit());
}
else
{
besked("FEJL:
du skal indtaste systemdata inden beregninger");
while
(!kbhit());
}
}
break;
case '4':
{
if
(data_inde)
{
optimer_n_m1_m2(1,
A, A1, A2, s, fkrav, faktuel, Wkrav, Waktuel, L, n, m1, m2, p0n, p00m1m2);
while
(!kbhit());
}
else
{
besked("FEJL:
du skal indtaste systemdata inden beregninger");
while
(!kbhit());
}
}
break;
case '5':
{
if
(data_inde)
{
optimer_n_m1_m2(2,
A, A1, A2, s, fkrav, faktuel, Wkrav, Waktuel, L, n, m1, m2, p0n, p00m1m2);
while
(!kbhit());
}
else
{
besked("FEJL:
du skal indtaste systemdata inden beregninger");
while
(!kbhit());
}
}
break;
}
} while (tast !=
'0');
// frigør de eksisterende matricer
if (data_inde)
{
free(*p0n);
free(p0n);
free(*p00m1m2);
free(p00m1m2);
}
}
|
|
|
Bilag 6.
Den vedlagte
diskette indeholder følgende:
PRO.ZIP Dette dokument pakket med
pkzip.
SIMUL.CPP Sourcekoden til
simuleringsprogrammet der er vist i bilag 5.
SIMUL.EXE Programmet SIMUL.EXE.